2023年12月31日
2023年12月27日
2023年12月23日
定義に従って三角関数の値を求める
(2)$\large\cos135°$
(3)$\large\tan210°$」
2023年12月17日
sin11.25°、cos11.25°、tan11.25°はどんな数?
2023年12月13日
この二重根号の等式は成り立っている?
「上の等式が成り立つことを証明せよ。」
2023年12月11日
15°、22.5°、67.5°、75°の三角比
2023年12月9日
中間角の三角関数
2023年12月7日
sin4.5°、cos4.5°、tan4.5°はどんな数?
2023年12月6日
18°、36°、54°、72°の三角比
$18°, 36°, 54°, 72°$の三角比はすべて1つの三角形を出発点として求めることができます。
2023年12月2日
恒等でないtanの半角の公式の変形
2023年11月30日
tanのとりうる値の範囲はなぜすべての実数なのか?
任意の実数$θ$において$\tanθ$のとりうる値の範囲はなぜすべての実数なのでしょうか?
2023年11月27日
三角関数 半角の公式
2023年11月25日
三角関数 2倍角の公式
2023年11月23日
三角関数の加法定理
これらはなぜ成り立つのでしょうか?
2023年11月21日
正負の数の足し算・引き算を数直線で考える
符号のない数の足し算
2023年11月13日
公約数についてこれは正しい?
2023年11月11日
1次不定方程式の整数解を求める(2)
(1)$\large37x+42y=3$
(2)$\large84x-56y=21$
(3)$\large39x+52y=12$」
2023年11月9日
公倍数は最小公倍数の倍数?
なぜ公倍数は最小公倍数の倍数となるのでしょうか?
中点連結定理の拡張の考察
中点連結定理を利用して次の性質を導くことができるでしょうか?
2023年10月31日
高低差からテーブルの高さを求める
- 花瓶Aを床に、花瓶Bをテーブルの上に置いたときの花瓶A、Bの高低差は$46$cm。
- 花瓶Bを床に、花瓶Cをテーブルの上に置いたときの花瓶B、Cの高低差は$58$cm$。
- 花瓶Cを床に、花瓶Aをテーブルの上に置いたときの花瓶A、Cの高低差は$40$cm。
2023年10月26日
三平方の定理の逆は成り立つ?
2023年10月23日
1次関数と反比例のグラフと三角形の面積
2023年10月9日
中点連結定理の逆は成り立つ?
中点連結定理は三角形のものと台形のものがありますが、それぞれの定理の逆は成り立つでしょうか?
2023年10月4日
なぜ0で割ってはいけないのかを引き算で考える
2023年9月30日
関数のグラフの平行移動
なぜこのように表すことができるのでしょうか?
2023年9月22日
方べきの定理の逆は成り立つ?
$\textbf{(a), (b)}:$ 2本の弦$\text{AB, CD}$、またはそれらの延長が点$\text{P}$で交わるとき、$\text{AP}\cdot \text{BP}=\text{CP}\cdot \text{DP}$が成り立つ。
$\textbf{(c)}:$ 点$\text{A}$を通る接線と弦$\text{BC}$の延長が点$\text{P}$で交わるとき、$\text{AP}^2=\text{BP}\cdot \text{CP}$が成り立つ。
では、方べきの定理の逆とはどういったものとなり、それは成り立つでしょうか?
2023年9月21日
接弦定理の逆は成り立つ?
この定理の逆はどういったもので、それは成り立つでしょうか?
2023年9月18日
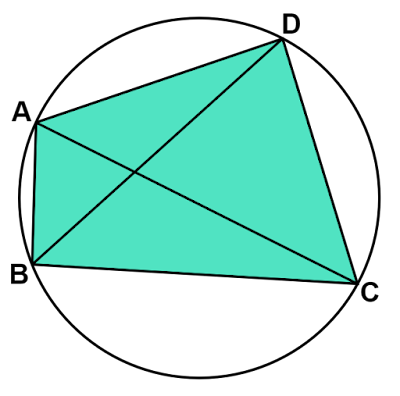
円に内接する四角形の対角の性質の逆は成り立つ?
なぜこれが成り立つのかを確かめてみます。
2023年9月17日
4点A,B,C,Dについて∠ACB=∠ADB=90°が成り立つとき必ず円周角の定理の逆は使えるか?
このとき、4点が同一円周上にあるといえる根拠は円周角の定理の逆だけでしょうか?
2023年9月15日
-(-3)はなぜ+3なのか? 数直線で考えてみる
2023年9月13日
正の数と負の数と絶対値
符号のない数
2023年9月8日
円周角の定理の逆 なぜ成り立つ?
1. 1つの弧に対する円周角の大きさは一定である。
2. 1つの弧に対する中心角の大きさは同じ弧に対する円周角の2倍である。
2023年9月3日
数直線で見る不等式を解く基本的な4つの操作
2023年8月27日
a<bのときa^2とb^2の大小関係はどうなる?
定数$a,b$について$a<b$のとき、$a^2$と$b^2$の大小関係はどうなるでしょうか?
2023年8月24日
2023年8月11日
円に内接する四角形の対辺のなす角の二等分線は直交する?
2023年8月9日
余弦定理とベクトル
ではここで、$\vec{\text{AB}},\vec{\text{AC}},\vec{\text{BC}}$というベクトルを考えたとき、余弦定理はベクトルでどのように表すことができるのでしょうか?
2023年8月6日
三角形の外心と垂心と重心の関係 オイラー線
これが成り立つことを確かめてみます。
2023年7月31日
三角形の外心と垂心の関係
上図のように頂点$\text{A}$とその対辺$\text{BC}$に着目した場合は、頂点$\text{A}$から垂心$\text{H}$までの距離$\text{AH}$と外心$\text{O}$から対辺$\text{BC}$までの距離$\text{OM}$の間には$\text{AH}=2\text{OM}$が成り立ちます。
これが成り立つことを鋭角三角形、直角三角形、鈍角三角形それぞれの場合にわけて確かめてみます。
2023年7月30日
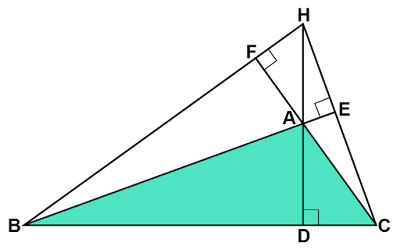
鈍角三角形の3本の垂線の性質
2023年7月26日
直角三角形の垂線の性質
したがって、直角三角形の垂線というと直角の頂点から引いたものしかないように見えます。上図の直角三角形$\text{ABC}$においては線分$\text{AD}$のことです。
この垂線にはどのような性質があるでしょうか?
2023年7月24日
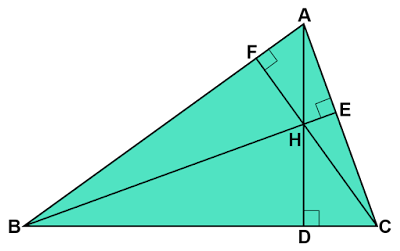
鋭角三角形の3本の垂線の性質
2023年7月22日
加法定理と正弦定理でトレミーの定理を証明してみる
これが成り立つことを、加法定理と正弦定理を利用して証明してみます。
2023年7月17日
スチュワートの定理
なぜこれが成り立つといえるのでしょうか?
2023年7月16日
中線定理 なぜ成り立つ?
なぜこれが成り立つといえるのでしょうか?
2023年7月13日
約分可能な有理関数のグラフは?
(1)$\large y=\dfrac{x^2}{x}$
(2)$\large y=\dfrac{(2x+3)(x+1)(x-2)}{x+1}$
(3)$\large y=\dfrac{x^3+4x^2-11x-30}{x^2-3x-10}$」
2023年7月9日
「AさんとBさんは嘘つき」の否定は?
「Aさん、Bさん、Cさんの3人からそれぞれ以下のような話を聞くことができた。
A:Cさんは正直者です。
B:Aさんは嘘つきです。
C:AさんとBさんは嘘つきです。
このような問題でCさんが嘘つきであると仮定したとき、Cさんの発言内容からわかることは何でしょうか?
2023年7月6日
-θ、90°±θ、180°±θ、270°±θの三角関数
| 角度 | $θ$のときの三角関数との関係 |
|---|---|
| $-θ$ | $\sin(-θ)=-\sinθ$ |
| $\cos(-θ)=\cosθ$ | |
| $\tan(-θ)=-\tanθ$ | |
| $90°-θ$ | $\sin(90°-θ)=\cosθ$ |
| $\cos(90°-θ)=\sinθ$ | |
| $\tan(90°-θ)=\dfrac{1}{\tanθ}$ | |
| $90°+θ$ | $\sin(90°+θ)=\cosθ$ |
| $\cos(90°+θ)=-\sinθ$ | |
| $\tan(90°+θ)=-\dfrac{1}{\tanθ}$ | |
| $180°-θ$ | $\sin(180°-θ)=\sinθ$ |
| $\cos(180°-θ)=-\cosθ$ | |
| $\tan(180°-θ)=-\tanθ$ | |
| $180°+θ$ | $\sin(180°+θ)=-\sinθ$ |
| $\cos(180°+θ)=-\cosθ$ | |
| $\tan(180°+θ)=\tanθ$ | |
| $270°-θ$ | $\sin(270°-θ)=-\cosθ$ |
| $\cos(270°-θ)=-\sinθ$ | |
| $\tan(270°-θ)=\dfrac{1}{\tanθ}$ | |
| $270°+θ$ | $\sin(270°+θ)=-\cosθ$ |
| $\cos(270°+θ)=\sinθ$ | |
| $\tan(270°+θ)=-\dfrac{1}{\tanθ}$ |
なぜこのような関係になるのでしょうか?
2023年6月29日
sin(ax+b)、cos(ax+b)、tan(ax+b)の周期
実関数$\sin(ax+b),\cos(ax+b),\tan(ax+b)$ $(a,b:実数;a\neq0)$の周期は何でしょうか?
2023年6月25日
三角関数の周期を求める
(1)$\large\sin2x$
(2)$\large\tan\bigl(-\sqrt{3}x\bigr)$
(3)$\large\cos\left(\dfrac{x}{3}-\dfrac{\pi}{6}\right)$」2023年6月21日
sin x^2は周期関数?
「$\sin x^2$が周期関数でないことを示せ。」
2023年6月15日
円の弦の垂直二等分線と中心
垂直二等分線上の点以外に等距離の点は存在する?
2023年6月10日
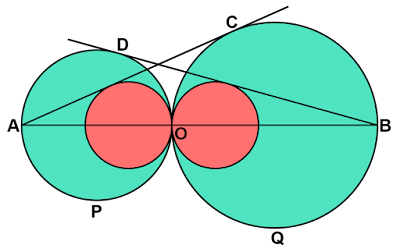
相似を利用して円の半径を求める
点$\text{A}$を通る円$\text{Q}$の接線と、点$\text{B}$を通る円$\text{P}$の接線を引き、それぞれの接点を$\text{C, D}$とする。
このとき、直線$\text{AB}$上に中心があり点$\text{O}$を通る円のうち、直線$\text{AC}$に接する円と直線$\text{BD}$に接する円の半径が等しいことを示せ。」
2023年6月7日
-3.14の整数部分は?(負の数の整数部分)
2023年6月6日
部分積分法
2023年6月2日
奇数の自然数を1から順に足すとなぜ平方数になるのか?
これは数式で
なぜこれが成り立つのでしょうか?
2023年5月29日
a+bとab/(a+b)はどちらが大きい?(2つの数の大小比較)
「$a>0,b>0$のとき$a+b$と$\dfrac{ab}{a+b}$はどちらが大きいか?
不等式で答えよ。」
2023年5月27日
アルキメデスの双子円の半径を求める
これが成り立つことを座標平面をもちいて確かめてみます。
2023年5月24日
床関数と天井関数
床関数
2023年5月17日
[x]([ ]:ガウス記号)の定積分
\[\int^3_2[x]\ dx\quad([\ ]:ガウス記号)\]
この定積分はどのような値となるでしょうか?
2023年5月10日
負の数のべき乗が実数となる条件は?
2023年5月3日
アルベロス図形とは
2023年5月2日
x^xの微分
これを微分するためには以下のような方法で行います。
2023年4月30日
2数、3数の場合の相加平均と相乗平均の大小関係
2023年4月28日
虚数単位と平方根の積の公式
虚数単位とは?
2023年4月25日
平方根とは? 平方根の計算法則
平方根とは?
このとき、$a$と$-a$は絶対値が等しい数です。また、$a^2$は必ず正の値を持ちます。
では逆に2乗して$a^2$になる数はなにかというと上記より$a$と$-a$の2つといえます。
この2乗して$a^2$になる$a$と$-a$のことを$a^2$の平方根といい、正の数$a$のことを正の平方根、負の数$-a$のことを負の平方根といいます。この2つをまとめて$\pm
a$とも書くことができます。
$0$の平方根は、2乗して$0$となる数は$0$のみであることから$0$ただ1つです。
2023年4月24日
f(x)=|x|を導関数にもつ関数を求める
2023年4月17日
未知数が3つある連立方程式を解く
2023年4月14日
投げ上げたボールの最高点を求める
「Aさんがボールを投げ上げたところ$2[\text{m}]$先にある高さ$3[\text{m}]$の塀の上にある瓶に当たった。
ボールがAさんから瓶までの地点間を$5:3$に内分する位置で最高点に到達したとき、最高点におけるボールの高さを求めよ。
ボールがAさんの手を離れた直後のボールの位置はAさんの頭上で高さは$2[\text{m}]$とし、瓶に当たるとはAさんから$2[\text{m}]$先、高さ$3[\text{m}]$の位置をボールの中心が通過する軌道を描いたものとする。
また、空気抵抗は無視する。」
2023年4月8日
三平方の定理を利用して四面体の辺の長さを求める
(1)$∠\text{BAC}=90°$
(2)$∠\text{AOB}=90°$」
2023年4月6日
連分数で表された数はどんな数?
(1)$3+\dfrac{1}{3+\frac{1}{3+\frac{1}{\ddots}}}$
(2)$-2+\dfrac{1}{2+\frac{1}{2+\frac{1}{\ddots}}}$」
このような問題はどのように解けばよいのでしょうか?
2023年4月2日
弧の長さと半径からおうぎ形の面積を求める
「半径が$4[\text{cm}]$、弧の長さが$7[\text{cm}]$であるおうぎ形の面積を求めよ。円周率は$\pi$とする。」
2023年3月25日
3次不等式を解く
(1)$\large (x+2)^3<8$
(2)$\large (x+1)^2(x-2)\leqq0$
(3)$\large x(x+2)(x-5)>0$」
2023年3月15日
楕円のy座標が最小となる点は?
このような問題はどのように解けばよいのでしょうか?
2023年3月11日
正八角形の面積を求める
2023年3月9日
三角形の重心とその性質
三角形には必ず重心が存在することと重心の性質について確かめてみます。
2023年3月3日
正多角形の内角と外角の大きさの比
正多角形の内角と外角の大きさの比はどのようになるのでしょうか?
多角形の内角の和の求め方 正多角形の1つの内角の大きさの求め方
また、正多角形の1つの内角の大きさはどのように求めるのでしょうか?
2023年2月27日
整数係数の3次方程式の有理数解の候補
2023年2月25日
おうぎ形はどれ?
2023年2月23日
三角形の垂心
2023年2月19日
三角形と台形の中点連結定理
なぜこれが成り立つのでしょうか?確かめてみます。
2023年2月18日
並列接続された抵抗全体の抵抗値の計算 (分数と逆数)
2023年2月14日
円周角と弧で囲まれた部分の面積は?
このとき線分$\text{AC, BC}$と弧$\text{AB}$で囲まれた部分の面積を求めよ。」
このような問題はどのように解けばよいのでしょうか?
2023年2月6日
相似な三角形の面積比はなぜ相似比の2乗となるのか?
2023年2月3日
正の約数の個数が奇数になるのはどんな数?
自然数の正の約数が奇数個になるのはどのような数なのでしょうか?
2023年2月2日
2023!と100^2023はどちらのほうが大きい?(2つの数の大小比較)
「$2023!$と$100^{2023}$はどちらのほうが大きいか?」
2023年1月30日
タレスの定理とその逆
これはなぜ成り立つのでしょうか?また、タレスの定理の逆についても考えます。
2023年1月28日
定義域で場合分けする2次関数の最大値・最小値を求め方
(1)$\large a\leqq x\leqq a+1$
(2)$\large a\leqq x<a+1$
(3)$\large a<x<a+1$」2023年1月25日
10年間複利で1000万円達成するのに最低限必要な元金は?
「年率$3.7$%、10年間複利で1000万円にするためには初めに最低何円預ける必要があるか?千の位まで答えよ。ただし、年率は一定で、税金、費用等はかからないものとする。」
2023年1月22日
底面積と表面積から円錐の高さを求める
このような問題はどのように解けばよいのでしょうか?
2023年1月21日
250!を素因数分解すると11はいくつある?
このような問題はどのように解けばよいのでしょうか?
2023年1月19日
1辺の長さが1の正六角形の幅と高さは?
2023年1月16日
1からa^nまでに含まれるaの倍数は何個?
「$a,n$を正の整数とする。$1$から$a^n$までの整数の中に$a$の倍数はいくつあるか?$a,n$をもちいて表わせ。」
2023年1月14日
3!!と(3!)!の違いは?
$3!!$と$(3!)!$はどちらも階乗を表していますが、この2つにはどんな違いがあるのでしょうか?
平行線と等間隔の点でつくる格子
$\text{A}_1$と$\text{C}_1$、$\text{A}_2$と$\text{C}_2$、$\text{A}_3$と$\text{C}_3$を直線$d, e, f$で結び、直線$b$との交点をそれぞれ$\text{B}_1, \text{B}_2, \text{B}_3$とすると、以下が成り立ちます。
2023年1月9日
外接円の半径と内角の1つがわかっている三角形の面積のとりうる値の範囲は?
「$∠\text{A}=135°$である三角形$\text{ABC}$は半径$3$の外接円を持つ。
この三角形の面積$S$のとりうる値の範囲を求めよ。」
2023年1月7日
2023^2023の下1桁は?
このような問題はどのように解けばよいのでしょうか?
2023年1月5日
2次関数のグラフ上の2点を通る直線のy切片を求める
このような問題はどのように解けばよいのでしょうか?
2023年1月3日
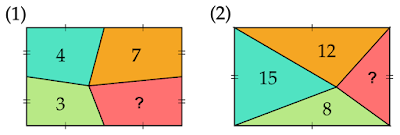
4つに分割された長方形の一部分の面積は?
2023年1月2日
2つの関数のグラフに挟まれた部分の面積
定積分はx軸より上側にある部分か下側にある部分かで正負が変わりますが、なぜx軸との位置関係に関係なくこの式で面積を求めることができるのでしょうか?
2023年1月1日
12^5の上2桁は何?
「$12^5$の上2桁を答えよ。
ただし、$2=10^{0.3010},3=10^{0.4771}$であることをもちいてよい。」

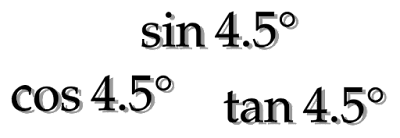
.png)
.png)

.png)

.png)



.png)




.png)





.png)

.png)
.png)
.png)


.png)
.png)

.png)



