角度が$-θ,90°±θ,180°±θ,270°±θ$それぞれのときの三角関数は角度$θ$のときの三角関数と以下のような関係にあります。
| 角度 | $θ$のときの三角関数との関係 |
|---|---|
| $-θ$ | $\sin(-θ)=-\sinθ$ |
| $\cos(-θ)=\cosθ$ | |
| $\tan(-θ)=-\tanθ$ | |
| $90°-θ$ | $\sin(90°-θ)=\cosθ$ |
| $\cos(90°-θ)=\sinθ$ | |
| $\tan(90°-θ)=\dfrac{1}{\tanθ}$ | |
| $90°+θ$ | $\sin(90°+θ)=\cosθ$ |
| $\cos(90°+θ)=-\sinθ$ | |
| $\tan(90°+θ)=-\dfrac{1}{\tanθ}$ | |
| $180°-θ$ | $\sin(180°-θ)=\sinθ$ |
| $\cos(180°-θ)=-\cosθ$ | |
| $\tan(180°-θ)=-\tanθ$ | |
| $180°+θ$ | $\sin(180°+θ)=-\sinθ$ |
| $\cos(180°+θ)=-\cosθ$ | |
| $\tan(180°+θ)=\tanθ$ | |
| $270°-θ$ | $\sin(270°-θ)=-\cosθ$ |
| $\cos(270°-θ)=-\sinθ$ | |
| $\tan(270°-θ)=\dfrac{1}{\tanθ}$ | |
| $270°+θ$ | $\sin(270°+θ)=-\cosθ$ |
| $\cos(270°+θ)=\sinθ$ | |
| $\tan(270°+θ)=-\dfrac{1}{\tanθ}$ |
なぜこのような関係になるのでしょうか?
単位円による三角関数の定義
まずは三角関数$\sinθ,\cosθ,\tanθ$が単位円上でどのように定義されているのかを見ていきます。
単位円とは半径が$1$の円のことで、特に三角関数においては座標平面上の原点を中心とする半径$1$の円のことを指します。
単位円の半径のうちx軸の正の部分から反時計回りを正の方向として$θ$の角をなしているものの単位円周上の点のx座標が$\cosθ$、y座標が$\sinθ$となります。
$\tanθ$はこの半径の延長と単位円上の点$(1,0)$で接する直線$x=1$との交点のy座標となります。
上でx軸の正の部分となる半直線を始線、始線とある角をなす半径を動径といいます。
単位円の半径のうちx軸の正の部分から反時計回りを正の方向として$θ$の角をなしているものの単位円周上の点のx座標が$\cosθ$、y座標が$\sinθ$となります。
$\tanθ$はこの半径の延長と単位円上の点$(1,0)$で接する直線$x=1$との交点のy座標となります。
上でx軸の正の部分となる半直線を始線、始線とある角をなす半径を動径といいます。
なす角を$θ$として$0°≦θ<360°$の範囲で考えたとき$θ=0°$の動径は始線、$θ=90°$の動径はy軸の正の部分、$θ=180°$の動径はx軸の負の部分、$θ=270°$の動径はy軸の負の部分と重なります。
$-θ$のときの三角関数
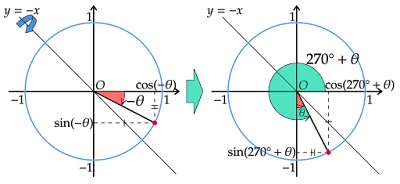
$θ$の動径は始線から反時計回りに$θ$だけ回転した半径ですが、$-θ$の動径は始線から時計回りに$θ$だけ回転した半径となります。
すなわち、$-θ$の動径と$θ$の動径は互いにx軸に関して対称な位置関係にあります。
$θ$の動径をx軸に関して対称移動して$-θ$の動径になると、動径である線分上の各点の座標はx座標は変化しませんが、y座標の正負が反転します。
すなわち、$-θ$の動径と$θ$の動径は互いにx軸に関して対称な位置関係にあります。
$θ$の動径をx軸に関して対称移動して$-θ$の動径になると、動径である線分上の各点の座標はx座標は変化しませんが、y座標の正負が反転します。
したがって、$-θ$のときの三角関数は$θ$のときの三角関数で表すと以下のようになります。
\begin{align*}\sin(-\theta)&=-\sin\theta\\[0.5em]\cos(-\theta)&=\cos\theta\\[0.5em]\tan(-\theta)&=-\tan\theta\end{align*}
$90°±θ$のときの三角関数
$90°-θ$のときの三角関数
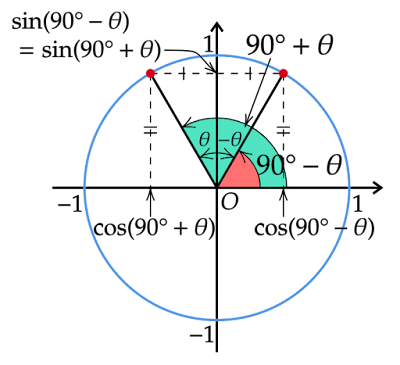
$90°-θ$の動径はy軸の正の部分から時計回りに$θ$だけ回転した半径であるといえます。
y軸の正の部分とx軸の正の部分(始線)は互いに直線$y=x$に関して対称な位置関係にあるので、$90°-θ$の動径と$θ$の動径も互いに直線$y=x$に関して対称な位置関係にあります。
$θ$の動径を直線$y=x$に関して対称移動して$90°-θ$の動径になると、動径である線分上の各点の座標はx座標とy座標が入れ替わります。
y軸の正の部分とx軸の正の部分(始線)は互いに直線$y=x$に関して対称な位置関係にあるので、$90°-θ$の動径と$θ$の動径も互いに直線$y=x$に関して対称な位置関係にあります。
$θ$の動径を直線$y=x$に関して対称移動して$90°-θ$の動径になると、動径である線分上の各点の座標はx座標とy座標が入れ替わります。
したがって、$\sin(90°-θ),\cos(90°-θ)$は以下のようになります。
\begin{align*}\sin(90°-\theta)&=\cos\theta\\[0.5em]\cos(90°-\theta)&=\sin\theta\end{align*}
$\tan(90°-θ)$については三角関数の相互関係を利用します。
三角関数の相互関係$\tan x=\dfrac{\sin x}{\cos x}$より
三角関数の相互関係$\tan x=\dfrac{\sin x}{\cos x}$より
\begin{align*}\tan(90°-\theta)&=\frac{\sin(90°-\theta)}{\cos(90°-\theta)}\\[0.5em]&=\frac{\cos\theta}{\sin\theta}\\[0.5em]&=\frac{1}{\tan\theta}\end{align*}
となります。
$90°+θ$のときの三角関数
$90°+θ$の動径はy軸の正の部分から反時計回りに$θ$だけ回転した半径であるといえるので、$90°+θ$の動径と$90°-θ$の動径は互いにy軸に関して対称な位置関係にあります。
$90°-θ$の動径をy軸に関して対称移動して$90°+θ$の動径になると、動径である線分上の各点の座標はy座標は変化しませんが、x座標の正負が反転します。
$90°-θ$の動径をy軸に関して対称移動して$90°+θ$の動径になると、動径である線分上の各点の座標はy座標は変化しませんが、x座標の正負が反転します。
したがって、$90°+θ$のときの三角関数は$θ$のときの三角関数で表すと以下のようになります。
\begin{align*}\sin(90°+\theta)&=\sin(90°-\theta)\\[0.5em]&=\cos\theta\\[1em]\cos(90°+\theta)&=-\cos(90°-\theta)\\[0.5em]&=-\sin\theta\\[1em]\tan(90°+\theta)&=\frac{\sin(90°+\theta)}{\cos(90°+\theta)}\\[0.5em]&=\frac{\cos\theta}{-\sin\theta}\\[0.5em]&=-\frac{1}{\tan\theta}\end{align*}
$180°±θ$のときの三角関数
$180°-θ$のときの三角関数
$180°-θ$の動径はx軸の負の部分から時計回りに$θ$だけ回転した半径であるといえます。
x軸の負の部分とx軸の正の部分(始線)は互いにy軸に関して対称な位置関係にあるので、$180°-θ$の動径と$θ$の動径も互いにy軸に関して対称な位置関係にあります。
$θ$の動径をy軸に関して対称移動すると、動径である線分上の各点の座標はy座標は変化しませんが、x座標の正負が反転します。
x軸の負の部分とx軸の正の部分(始線)は互いにy軸に関して対称な位置関係にあるので、$180°-θ$の動径と$θ$の動径も互いにy軸に関して対称な位置関係にあります。
$θ$の動径をy軸に関して対称移動すると、動径である線分上の各点の座標はy座標は変化しませんが、x座標の正負が反転します。
したがって、$180°-θ$のときの三角関数は$θ$のときの三角関数で表すと以下のようになります。
\begin{align*}\sin(180°-\theta)&=\sin\theta\\[0.5em]\cos(180°-\theta)&=-\cos\theta\\[1em]\tan(180°-\theta)&=\frac{\sin(180°-\theta)}{\cos(180°-\theta)}\\[0.5em]&=\frac{\sin\theta}{-\cos\theta}\\[0.5em]&=-\tan\theta\end{align*}
$180°+θ$のときの三角関数
$180°+θ$の動径はx軸の負の部分から反時計回りに$θ$だけ回転した半径であるといえるので、$180°+θ$の動径と$180°-θ$の動径は互いにx軸に関して対称な位置関係にあります。
$180°-θ$の動径をx軸に関して対称移動すると、動径である線分上の各点の座標はx座標は変化しませんが、y座標の正負が反転します。
$180°-θ$の動径をx軸に関して対称移動すると、動径である線分上の各点の座標はx座標は変化しませんが、y座標の正負が反転します。
したがって、$180°+θ$のときの三角関数は$θ$のときの三角関数で表すと以下のようになります。
\begin{align*}\sin(180°+\theta)&=-\sin(180°-\theta)\\[0.5em]&=-\sin\theta\\[1em]\cos(180°+\theta)&=\cos(180°-\theta)\\[0.5em]&=-\cos\theta\\[1em]\tan(180°+\theta)&=-\tan(180°-\theta)\\[0.5em]&=\tan\theta\end{align*}
$270°±θ$のときの三角関数
$270°-θ$のときの三角関数
$270°-θ$の動径はy軸の負の部分から時計回りに$θ$だけ回転した半径であるといえます。
y軸の負の部分とx軸の正の部分(始線)は互いに直線$y=-x$に関して対称な位置関係にあるので、$270°-θ$の動径は$θ$の動径も互いに直線$y=-x$に関して対称な位置関係にあります。
$θ$の動径を直線$y=-x$に関して対称移動すると、動径である線分上の各点の座標はx座標とy座標が入れ替わり、かつ正負が反転します。
y軸の負の部分とx軸の正の部分(始線)は互いに直線$y=-x$に関して対称な位置関係にあるので、$270°-θ$の動径は$θ$の動径も互いに直線$y=-x$に関して対称な位置関係にあります。
$θ$の動径を直線$y=-x$に関して対称移動すると、動径である線分上の各点の座標はx座標とy座標が入れ替わり、かつ正負が反転します。
したがって、$270°-θ$のときの三角関数は$θ$のときの三角関数で表すと以下のようになります。
\begin{align*}\sin(270°-\theta)&=-\cos\theta\\[0.5em]\cos(270°-\theta)&=-\sin\theta\\[0.5em]\tan(270°-\theta)&=\frac{\sin(270°-\theta)}{\cos(270°-\theta)}\\[0.5em]&=\frac{-\cos\theta}{-\sin\theta}\\[0.5em]&=\frac{1}{\tan\theta}\end{align*}
$270°+θ$のときの三角関数
$270°+θ$の動径はy軸の負の部分から反時計回りに$θ$だけ回転した半径であるといえます。
$270°+θ$の動径は$-θ$の動径と互いに直線$y=-x$に関して対称な位置関係にあります。
$-θ$の動径を直線$y=-x$に関して対称移動すると、動径である線分上の各点の座標はx座標とy座標が入れ替わり、かつ正負が反転します。
$270°+θ$の動径は$-θ$の動径と互いに直線$y=-x$に関して対称な位置関係にあります。
$-θ$の動径を直線$y=-x$に関して対称移動すると、動径である線分上の各点の座標はx座標とy座標が入れ替わり、かつ正負が反転します。
したがって、$270°+θ$のときの三角関数は$θ$のときの三角関数で表すと以下のようになります。
\begin{align*}\sin(270°+\theta)&=-\cos(-\theta)\\[0.5em]&=-\cos\theta\\[1em]\cos(270°+\theta)&=-\sin(-\theta)\\[0.5em]&=\sin\theta\\[1em]\tan(270°+\theta)&=\frac{\sin(270°+\theta)}{\cos(270°+\theta)}\\[0.5em]&=\frac{-\cos\theta}{\sin\theta}\\[0.5em]&=-\frac{1}{\tan\theta}\end{align*}
(2026/1)加筆しました。
Share:
.png)
.png)
.png)
.png)
.png)