半径$1$の円に内接・外接する正三角形の周の長さはいくらになるのかを計算してみます。
円周と正三角形の周の長さの関係から円周率の値がどのくらい絞り込めるのかも調べてみます。
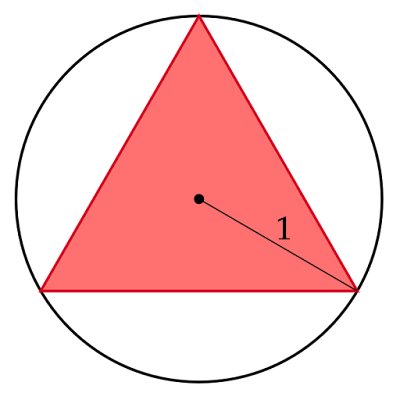
円に内接する正三角形
正三角形の重心の性質として、中線を$2:1$に内分するというものがあります。
そして、正三角形の中線で2等分されることによってできる直角三角形の3辺の長さの比は以下の図のようになります。
この比を利用して正三角形の1辺の長さを$x$として求めると、
.png)
|
| 図 $30°-60°-90°$の直角三角形の三角比 |
\begin{align*}\sqrt{3}:2&=\frac{3}{2}:x\\[0.5em]\sqrt{3}x&=3\\[0.5em]x&=\sqrt{3}\end{align*}
となります。
したがって、半径1の円に内接する正三角形の周の長さはこの3倍の$\mathbf{3\sqrt{3}}$となります。
別の方法として、正弦定理を使う方法があります。
正弦定理より、円に内接する正三角形の1辺の長さ$x$は
\begin{align*}2&=\frac{x}{\sin60^{\circ}}\\[0.5em]x&=2\sin60^{\circ}\\[0.5em]&=2×\frac{\sqrt{3}}{2}\\[0.5em]&=\sqrt{3}\end{align*}
となるので、このことからも円に内接する正三角形の周の長さは$3\sqrt{3}$となることがわかります。
円とその円に内接する正三角形の周の長さを比較すると円周のほうが長いので
\begin{align*}2\pi&>3\sqrt{3}\\[0.5em]\therefore\pi&>\frac{3\sqrt{3}}{2}≒2.60\tag1\end{align*}
となります。すなわち、円周率$\pi$は$\dfrac{3\sqrt{3}}{2}$(およそ$2.60$)より大きいことがわかります。
円に外接する正三角形
円に内接する正三角形のときと同様に正三角形の中線を引きます。
すると、上図のような直角三角形ができます。この直角三角形は$30°-60°-90°$の直角三角形で、内心の性質より直角の三角形の短辺の長さは内接円の半径に等しいため$1$です。
正三角形の1辺の長さを$y$とすると、直角三角形の長辺の長さは$\dfrac{1}{2}y$なので
\begin{align*}1:\sqrt{3}&=1:\frac{1}{2}y\\[0.5em]\frac{1}{2}y&=\sqrt{3}\\[0.5em]y&=2\sqrt{3}\end{align*}
となります。
したがって、円に外接する正三角形の周の長さはこの3倍の$\mathbf{6\sqrt{3}}$となります。
円とその円に外接する正三角形の周の長さを比較すると円周のほうが短いので
\begin{align*}2\pi&<6\sqrt{3}\\[0.5em]\therefore\pi&<3\sqrt{3}≒5.20\tag2\end{align*}
となります。すなわち、円周率$\pi$は$3\sqrt{3}$(およそ$5.20$)より小さいことがわかります。
$(1),(2)$より、円に内接・外接する正三角形の周の長さからわかる円周率$\pi$のとりうる値の範囲は$\mathbf{\dfrac{3\sqrt{3}}{2}<\pi<3\sqrt{3}}$、すなわちおよそ$2.60$より大きくおよそ$5.20$より小さいことがわかります。
(2024/3)内容を修正しました。
Share:
.png)
.png)
.png)



