直交する弦の長さから円の半径を求める

　円の中心を通らない直交する2本の弦$\text{AB,CD}$の各部分の長さのみがわかっているとき、円の半径を求めるにはどうすればよいでしょうか?
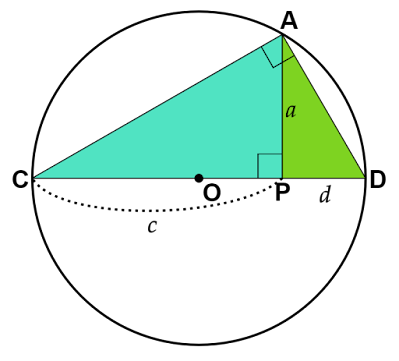
このとき、弦$\text{AB,CD}$の交点を$\text{P}$、線分$\text{AP,BP,CP,DP}$の長さをそれぞれ$a,b,c,d$、上図のように$a>b,c>d$であるとします。

導出

　中心$\text{O}$から各弦へ垂線をおろします。弦$\text{AB,CD}$上の垂線の足をそれぞれ$\text{Q,R}$とします。

中心$\text{O}$から引いた垂線は弦を二等分するので

$$\begin{align*}\text{AQ}=\text{QB}&=\frac{1}{2}\text{AB}\\[0.5em]&=\frac{a+b}{2}\\[1em]\text{CR}=\text{RD}&=\frac{1}{2}\text{CD}\\[0.5em]&=\frac{c+d}{2}\end{align*}$$

となります。

半径$\text{OA}$を引いてできる$△\text{OAQ}$は辺$\text{OA}$を斜辺とする直角三角形です。$\text{AQ}$の長さは上記の通り、四角形$\text{OQPR}$は長方形なので$\text{QO}=\text{PR}$より

$$\begin{align*}\text{QO}&=\text{PR}\\[0.5em]&=\text{CP}-\text{CR}\\[0.5em]&=c-\frac{c+d}{2}\\[0.5em]&=\frac{2c-(c+d)}{2}\\[0.5em]&=\frac{c-d}{2}\end{align*}$$

となります。

半径の長さを$r$とおき三平方の定理より

$$\begin{align*}r^2&=\text{AQ}^2+\text{QO}^2\\[0.5em]&=\left(\frac{a+b}{2}\right)^2+\left(\frac{c-d}{2}\right)^2\\[0.5em]&=\frac{(a+b)^2}{4}+\frac{(c-d)^2}{4}\\[0.5em]&=\frac{(a+b)^2+(c-d)^2}{4}\\[1em]r&=\frac{\sqrt{(a+b)^2+(c-d)^2}}{2}&(\because r>0)\end{align*}$$

となり、弦の長さから円の半径を求める式を導くことができます。

関連：三平方の定理（ピタゴラスの定理）

　例えば円$\text{O}$の直交する弦$\text{AB,CD}$の交点を$\text{P}$としたとき、$\text{AP}=3,\text{BP}=2,$$\text{CP}=6,\text{DP}=1$となった場合は、円$\text{O}$の半径$r$は

$$\begin{align*}r&=\frac{\sqrt{(3+2)^2+(6-1)^2}}{2}\\[0.5em]&=\frac{\sqrt{50}}{2}\\[0.5em]&=\frac{5\sqrt{2}}{2}\end{align*}$$

と求められます。

ちなみに直交する弦の各部分の長さが確かに上記のようになることがあるかは以下のように確かめられます。

$$\begin{align*}\text{AP}\cdot \text{BP}&=3\cdot2\\[0.5em]&=6\\[1em]\text{CP}\cdot \text{DP}&=6\cdot1\\[0.5em]&=6\end{align*}$$

より$\text{AP}\cdot \text{BP}=\text{CP}\cdot \text{DP}$が成り立つので方べきの定理の逆より4点$\text{A,B,C,D}$は同一円周上にあります。

関連：方べきの定理の逆は成り立つ？

したがって、確かに直交する円の弦の各線分の長さが$\text{AP}=3,\text{BP}=2,$$\text{CP}=6,\text{DP}=1$となることがあるとわかります。

弦が円の中心を通る場合

　また、弦のいずれかが円の中心を通る場合も

$$\begin{equation}\large r=\frac{\sqrt{(a+b)^2+(c-d)^2}}{2}\end{equation}$$

が成り立ちます。

弦の1本が円の中心を通る場合

　弦$\text{AB}$が円$\text{O}$の中心を通る場合、弦$\text{AB}$は円$\text{O}$の直径なので、半径の長さは$r=\dfrac{a+b}{2}$となります。

また、弦$\text{AB}$は弦$\text{CD}$の垂直二等分線となる、すなわち点$\text{P}$は弦$\text{CD}$の中点となるので、$c=d$が成り立ちます。

したがって、$(1)$より

$$\begin{align*}r&=\frac{\sqrt{(a+b)^2+(c-c)^2}}{2}\\[0.5em]&=\frac{\sqrt{(a+b)^2}}{2}\\[0.5em]&=\frac{|a+b|}{2}\\[0.5em]&=\frac{a+b}{2}&(\because a>0,b>0\Rightarrow a+b>0)\end{align*}$$

となり、成り立っていることがわかります。

関連：平方根とは？　平方根の計算法則

　次に弦$\text{CD}$が円$\text{O}$の中心を通る場合を考えます。弦$\text{CD}$は円$\text{O}$の直径なので、半径の長さは$r=\dfrac{c+d}{2}$となります。

また、弦$\text{CD}$は弦$\text{AB}$の垂直二等分線となる、すなわち点$\text{P}$は弦$\text{AB}$の中点となるので、$a=b$が成り立ちます。

したがって、$(1)$より

$$\begin{align*}r&=\frac{\sqrt{(a+a)^2+(c-d)^2}}{2}\\[0.5em]&=\frac{\sqrt{4a^2+(c-d)^2}}{2}\\[0.5em]&=\frac{\sqrt{4a^2+c^2+d^2-2cd}}{2}\tag2\end{align*}$$

となり、$r=\dfrac{c+d}{2}$になりそうに見えません。

しかし、線分$\text{AC,AD}$を引き、$△\text{ACP}$と$△\text{ADP}$に着目すると

これらは直角三角形なので$∠\text{APC}=∠\text{DPA}=90°\cdots\text{(a)}$

直角三角形$\text{ACP}$の直角以外の内角の和は$90°$なので、$∠\text{ACP}+∠\text{CAP}=90°$
すなわち$∠\text{ACP}=90°-∠\text{CAP}\ \cdots\text{(b)}$

タレスの定理より$∠\text{CAD}=∠\text{CAP}+∠\text{DAP}=90°$なので、$∠\text{DAP}=90°-∠\text{CAP}\ \cdots\text{(c)}$

関連：タレスの定理とその逆

$\text{(b),(c)}$より$∠\text{ACP}=∠\text{DAP}\cdots\text{(d)}$

$\text{(a),(d)}$より2組の角がそれぞれ等しいので$△\text{ACP}$と$△\text{ADP}$は相似であることがわかります。

相似比より

$$\begin{align*}\text{CP}:\text{AP}&=\text{AP}:\text{DP}\\[0.5em]c:a&=a:d\\[0.5em]\therefore a^2&=cd\end{align*}$$

となるので、$(2)$に代入すると

$$\begin{align*}r&=\frac{\sqrt{4cd+c^2+d^2-2cd}}{2}\\[0.5em]&=\frac{\sqrt{c^2+d^2+2cd}}{2}\\[0.5em]&=\frac{\sqrt{(c+d)^2}}{2}\\[0.5em]&=\frac{|c+d|}{2}\\[0.5em]&=\frac{c+d}{2}&(\because c>0,d>0\Rightarrow c+d>0)\end{align*}$$

となり、弦$\text{CD}$が円$\text{O}$の中心を通る場合においても$(1)$が成り立つことがわかります。

両方の弦が円の中心を通る場合

　弦$\text{AB,CD}$がともに円$\text{O}$の中心を通る場合、弦$\text{AB,CD}$は円の中心$\text{O}$で交わる、すなわち交点$\text{P}$と中心$\text{O}$は同一の点となるので線分$\text{AP,BP,CP,DP}$はすべて半径であり、$r=a=b=c=d$となります。

したがって、$(1)$より

$$\begin{align*}r&=\frac{\sqrt{(a+a)^2+(a-a)^2}}{2}&(\because a=b=c=d)\\[0.5em]&=\frac{\sqrt{4a^2}}{2}\\[0.5em]&=|a|\\[0.5em]&=a&(\because a>0)\end{align*}$$

となり、確かに成り立っていることがわかります。

以上より、円の直交する2本の弦$\text{AB,CD}$が直交していれば必ず

$$\large r=\frac{\sqrt{(a+b)^2+(c-d)^2}}{2}$$

が成り立つことがわかります。

(2024/2)内容を修正しました。