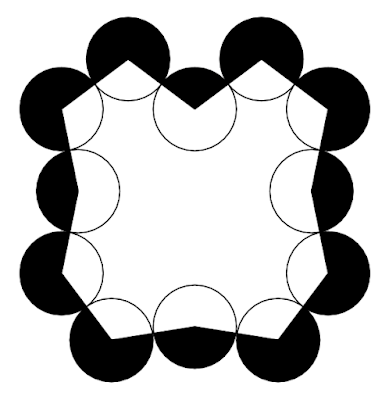
 |
| 図1 鎖の輪状に連なる円 |
「図1のように同じ半径の円が鎖の輪のように連なっている。それぞれの円の中心を線でつないでできる図形の内側にある方を白く、外側にある方を黒く円を塗り分けた。円の黒い部分の合計と白い部分の合計の面積の差はいくらになるか。1つの円の面積を1とする。」
まずは、半径の同じ円が鎖の輪状に連なる条件を考えてみます。
鎖の輪状に連なる条件とは、
- 隣り合う円と接していて交わらないこと
- すべての円が少なくとも2つの異なる円と接していること
ですが、わかりやすい特徴は隣接する円の中心をつなぐとすべての辺が等しい多角形ができることでしょう。
その条件のもと、どんな円の数や連なり方の場合でも成立する法則性や共通点を探ります。
 |
| 図2 4つの円が輪状に連なる |
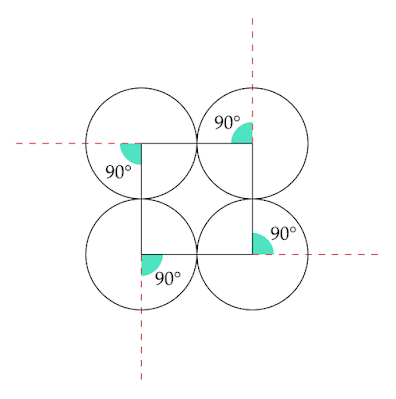
シンプルな形状として、4つの円が連なっている場合を考えます。
それぞれの円の中心をつなぐと正方形ができあがります。
外角に着目すると、90°が4つで和が360°になります。他の図形でも同様に360°で一定です。
これは多角形を対角線が交わらないように三角形で分割しきった時、内角の和が、
\begin{align*}(内角の和)&=(三角形の内角の和)×\left\{(頂点の数)-2\right\}\\ &=180^{\circ}×\left\{(頂点の数)-2\right\}\end{align*}
外角の和が、
\[(外角の和)=180^{\circ}×(頂点の数)-(内角の和)\]
すなわち、
\begin{align*}(外角の和)&=180^{\circ}×(頂点の数)-180^{\circ}×\left\{(頂点の数)-2\right\}\\ &=180^{\circ}×2=360^{\circ}\end{align*}
となるからです。
ただし、1つの内角には外角が2つありますが、1つの外角にのみ着目した場合です。
凹部がある図形でもこれは成り立ちます。
 |
| 図3 凹部のある円の連なり方 |
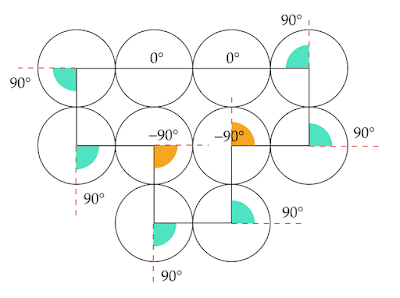
図3のような場合、凹部の外角が図形の内側にあると考え、負の角度とすることで外角の和が360°となります。
以上から、凹部の有無に関わらずあらゆる多角形の外角の和が360°となるので、問題の図形における外角の和も360°であるとわかります。
 |
| 図4 円を分割する扇形の面積の差分 |
また、1つの頂点の内角と外角の和が180°なので、1つの円に着目すると、円を直径で分割したときより外角の分だけ外側の面積が増え、内側の面積が減っていることがわかります。
外角の和が360°であるため、外側の面積は円1つ分増え、内側の面積は円1つ分減っています。
したがって、問題の円の黒い部分と白い部分の面積の差分は円2つ分、円1つの面積は1なので答えは2となります。
Share:
