.png)
しかし、作図の場合は3辺の垂直二等分線の交点として求められます。
なぜ、頂点からの距離が等しいという性質がありながら垂直二等分線で作図するのでしょうか？
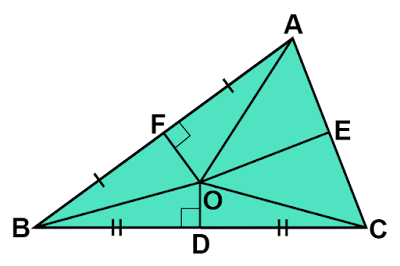
$△\text{AOF}$と$△\text{BOF}$に着目すると
点$\text{F}$は$\text{AB}$の中点なので$\text{AF}=\text{BF}$です。
$\text{OF}$は共通な辺なので$\text{OF}=\text{OF}$です。
また、$\text{OF}$は$\text{AB}$の垂直二等分線なので$∠\text{OFA}=∠\text{OFB}=90°$です。
したがって、2組の辺とその間の角がそれぞれ等しいので$△\text{AOF}$と$△\text{BOF}$は合同であり、$\text{OA}=\text{OB}$であることがわかります。
$△\text{BOD}$と$△\text{COD}$に着目すると
点$\text{D}$は$\text{BC}$の中点なので$\text{BD}=\text{CD}$です。
$\text{OD}$は共通な辺なので$\text{OD}=\text{OD}$です。
また、$\text{OD}$は$\text{BC}$の垂直二等分線なので$∠\text{ODB}=∠\text{ODC}=90°$です。
したがって、2組の辺とその間の角がそれぞれ等しいので$△\text{BOD}$と$△\text{COD}$は合同であり、$\text{OB}=\text{OC}$であることがわかります。
以上より$\text{OA}=\text{OB}=\text{OC}$であることがわかります。
ここで$△\text{AOE}$と$△\text{COE}$に着目すると
先ほどの結論より$\text{OA}=\text{OC}$です。
$\text{OE}$は共通な辺なので$\text{OE}=\text{OE}$です。
点$\text{E}$は$\text{CA}$の中点なので$\text{AE}=\text{CE}$です。
したがって、3組の辺がそれぞれ等しいので$△\text{AOE}$と$△\text{COE}$は合同であり、$∠\text{AEO}=∠\text{CEO}$で$∠\text{AEC}=180°$より$∠\text{AEO}=∠\text{CEO}=90°$、すなわち$\text{OE}$は$\text{CA}$の垂直二等分線であることがわかります。
以上より、三角形の3辺の垂直二等分線はただ1点で交わることがわかります。
また、$\text{OA}=\text{OB}=\text{OC}$よりこの点$\text{O}$は各頂点までの距離が等しいので、$\text{O}$を中心として三角形に外接する円を描くことができます。三角形の外接円の中心点とは、つまり外心のことです。
よって、三角形の3辺の垂直二等分線の交点が外心になることを示すことができました。
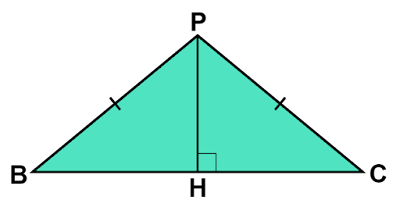
$\text{PH}⊥\text{BC}$より$∠\text{PHB}=∠\text{PHC}=90°$です。
点$\text{P}$は$\text{B, C}$から等距離なので$\text{BP}=\text{CP}$です。
$\text{PH}$は共通な辺なので$\text{PH}=\text{PH}$です。
したがって、$△\text{BPH}$と$△\text{CPH}$は合同であり、$\text{BH}=\text{CH}$であることがわかります。
それ以外の方法で3つの頂点からの距離が等しいという性質から外心を求めようとすると、等しい距離とはどれくらいの長さなのか？、頂点からどの方向へ直線をのばせばよいか？という問題が出てきます。
しかし、各辺の垂直二等分線上に外心が存在することを利用すれば、最低2辺の垂直二等分線を作図するだけで容易に外心の位置を知ることができます。
