- 2辺の長さが等しい。
- 2つの内角の大きさが等しい。
- 頂点から底辺へ引く垂線は垂直二等分線かつ頂角の二等分線になる。
1.の特徴は名称通り、定義通りのものですが、なぜ2.、3.の特徴を持つ三角形も二等辺三角形であると言えるのでしょうか？
.png)
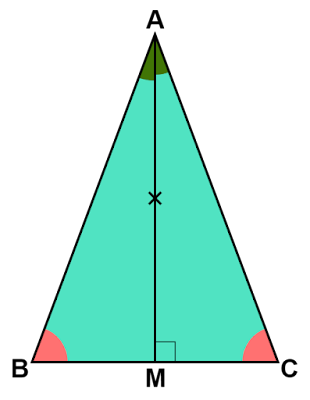
$\text{AM}⊥\text{BC}$より、$∠\text{AMB}=∠\text{AMC}=90°$なので、$△\text{ABM}$と$△\text{ACM}$は直角三角形となります。
$△\text{ABC}$は二等辺三角形であるから$\text{AB}=\text{AC}$。これは$△\text{ABM}$と$△\text{ACM}$それぞれの斜辺となります。
垂線$\text{AM}$は共通な辺となるので、$\text{AM}=\text{AM}$
また、$\text{BM}=\text{CM, }\
\text{AM}⊥\text{BC}$より垂線$\text{AM}$は$\text{BC}$の垂直二等分線であり、$∠\text{BAM}=∠\text{CAM}$であることから$\text{AM}$は頂角$∠\text{A}$の二等分線でもあることがわかります。
したがって、3.の特徴があることがわかります。
2.の特徴を持つ三角形
$∠\text{ABC}=∠\text{ACB}$より$∠\text{ABM}=∠\text{ACM}\ \cdots\text{(i)}$。
$\text{AM}⊥\text{BC}$より、$∠\text{AMB}=∠\text{AMC}=90°\
\cdots\text{(ii)}$。
$\text{(i), (ii)}$より$∠\text{BAM}=∠\text{CAM}\
\cdots\text{(iii)}$
また、$\text{AM}$は共通な辺なので、$\text{AM}=\text{AM}\
\cdots\text{(iv)}$。
$\text{(ii), (iii), (iv)}$より1組の辺とその両端の角がそれぞれ等しいので、$△\text{ACM}$と$△\text{BCM}$は合同であることがわかります。
3.の特徴を持つ三角形
線分とその垂直二等分線上の点によってできる三角形
.png)
$\text{AB}⊥\text{CM}$より、$∠\text{AMC}=∠\text{BMC}=90°$
点$\text{M}$は$\text{AB}$の中点であるから$\text{AM}=\text{BM}$
$\text{CM}$は共通な辺なので$\text{CM}=\text{CM}$
2組の辺とその間の角がそれぞれ等しいので$△\text{ACM}$と$△\text{BCM}$は合同であることがわかります。
2直線とそのなす角の二等分線の垂線によってできる三角形
.png)
$\text{AP}$は直線$l, m$のなす角の二等分線より$∠\text{BAP}=∠\text{CAP}$
$\text{AP}⊥\text{BC}$より$∠\text{APB}=∠\text{APC}=90°$
$\text{AP}$は共通の辺なので$\text{AP}=\text{AP}$
1組の辺とその両端の角がそれぞれ等しいので$△\text{ABP}$と$△\text{ACP}$は合同であることがわかります。
