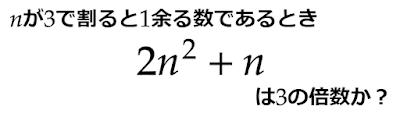「$n$は整数で3で割ると1余る。$2n^2+n$が3の倍数であることを示せ。」
3通りの方法で3の倍数であることを示してみます。
$n$が3で割ると1余る整数であることは、整数$k$をもちいて
\[n=3k+1\]
と表せることを利用します。
1. そのまま代入する
$2n^2+n$に代入すると
\begin{align*}2n^2+n&=2(3k+1)^2+(3k+1)\\[0.5em]&=2(9k^2+6k+1)+3k+1\\[0.5em]&=18k^2+12k+2+3k+1\\[0.5em]&=18k^2+15k+3\\[0.5em]&=3(6k^2+5k+1)\end{align*}
$6k^2+5k+1$は整数なので、$3(6k^2+5k+1)$は3の倍数であることがわかります。
したがって、$n$が3で割ると1余る整数であるとき、$2n^2+n$は3の倍数であることを示すことができました。
2. 因数分解してから代入する
$2n^2+n$は因数分解すると
\[2n^2+n=n(2n+1)\]
となります。これに$k$の式を代入すると
\begin{align*}n(2n+1)&=(3k+1){2(3k+1)+1}\\[0.5em]&=(3k+1)(6k+3)\\[0.5em]&=3(3k+1)(2k+1)\end{align*}
$(3k+1)(2k+1)$は整数なので、$3(3k+1)(2k+1)$は3の倍数であることがわかります。
したがって、$n$が3で割ると1余る整数であるとき、$2n^2+n$は3の倍数であることを示すことができました。
3. 合同式を利用
$n$が3で割ると1余る整数であることは、合同式では
\begin{equation}n\equiv1\quad(\text{mod}\ 3)\end{equation}
と書けます。これを合同式の性質にしたがって変形していきます。
合同式は両辺を2乗しても成り立つので
\begin{equation}n^2\equiv1\quad(\text{mod}\ 3)\end{equation}
また、両辺を2倍しても成り立つので
\begin{equation}2n^2\equiv2\quad(\text{mod}\ 3)\end{equation}
同じ数を法とする合同式の$(1),(3)$の辺々を加えても成り立つので
\[2n^2+n\equiv2+1=3\quad(\text{mod}\ 3)\]
右辺が$\text{mod}$の数の倍数のときは
\[2n^2+n\equiv0\quad(\text{mod}\ 3)\]
となります。
$3$を法とする合同式の右辺が$0$になるということは左辺の$2n^2+n$が3の倍数であるということです。
したがって、$n$が3で割ると1余る整数であるとき、$2n^2+n$は3の倍数であることを示すことができました。
Share: