.png)
2点$(a_1,a_2),(b_1,b_2)$を通る直線の方程式は
\[y=\frac{b_2-a_2}{b_1-a_1}(x-a_1)+a_2\]
となることを利用して求めると、x切片が$a$、y切片が$b$ということは2点$(a,0),(0,b)$を通るということなので直線の方程式は
\begin{align*}y&=\frac{b-0}{0-a}(x-a)+0\\[0.5em]y&=-\frac{b}{a}(x-a)\\[0.5em]y&=-\frac{b}{a}x+b\end{align*}
となります。
このように2点の座標がわかっている場合の直線の方程式の公式から求めることができますが、x切片とy切片だけがわかっている場合には直線の方程式の公式にはもう1つあります。
x切片が$a$、y切片が$b$である直線の方程式は、
x切片が$a$、y切片が$b$である直線の方程式は、
\[\Large\frac{x}{a}+\frac{y}{b}=1\]
で表すことができます。
x切片が$a$であるということは、直線は$(a,0)$を通るということで、この座標を代入すると
\begin{align*}\frac{a}{a}+\frac{0}{b}&=1\\[0.5em]1&=1\end{align*}
となり、成り立ちます。
また、y切片が$b$であるということは、直線は$(0,b)$を通るということで、この座標を代入すると
\begin{align*}\frac{0}{a}+\frac{b}{b}&=1\\[0.5em]1&=1\end{align*}
となり、成り立ちます。
このようにx切片、y切片の座標を代入すると左辺の2つの項のうち1つが消え、もう1つが$1$になるように方程式がつくられています。
直線は2点により1つに定まるので、2点の座標を代入して成り立つこの直線の方程式は、確かにx切片が$a$、y切片が$b$となる直線のものであることがわかります。
直線の方程式として示すとき、このままの形でも良いのですが、1次関数の形に直したい場合は$y$について解きます。
\begin{align*}\frac{bx}{a}+y&=b\\[0.5em]y&=-\frac{bx}{a}+b\\[0.5em]y&=-\frac{b}{a}x+b\end{align*}
すると、上で2点を通る直線の方程式の公式から求めたものと同じ形にすることができます。
実際にグラフから直線の方程式を求めてみます。
上のグラフの直線はx切片が$1$、y切片が$3$となっています。
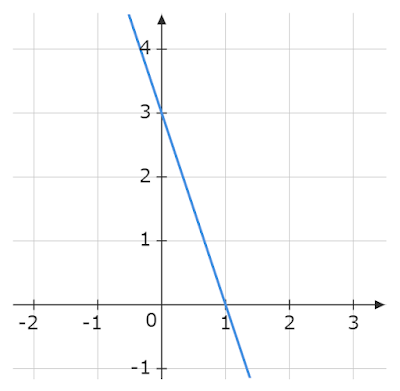
したがって、この直線の方程式は
1次関数の形にすると
\begin{align*}\frac{x}{1}+\frac{y}{3}&=1\\[0.5em]x+\frac{y}{3}&=1\end{align*}
となります。
1次関数の形にすると
\begin{align*}3x+y&=3\\[0.5em]y&=-3x+3\end{align*}
となります。
.png)
したがって、この直線の方程式は
1次関数の形にすると
\begin{align*}\frac{x}{-4}+\frac{y}{-2}=1\\[0.5em]-\frac{x}{4}-\frac{y}{2}&=1\\[0.5em]\frac{x}{4}+\frac{y}{2}&=-1\end{align*}
となります。公式と同じ形の式は1行目のものですが、3行目のように$x$の係数が正になるように変形することもできます。
1次関数の形にすると
\begin{align*}\frac{x}{2}+y&=-2\\[0.5em]y&=-\frac{x}{2}-2\\
&\left(またはy=-\frac{1}{2}x-2\right)\end{align*}
となります。
Share:
