1次関数（グラフの形、傾き、y切片）

　1次関数とは、

$$y=ax+b\qquad(a,b:実数,a\neq0)$$

という$y$が変数$x$についての次数が$1$の多項式によって表される関数のことです。

$a$は傾き、$b$はy切片といいます。$a=0$のときは基本的に1次関数には含まれません。

特に$b=0$のときの1次関数は$y=ax$で、これは$y$が$x$と比例の関係にあることを表します。このときの$a$は比例定数とも呼ばれます。

比例とは、$x$が2倍、3倍…に変化するにともなって$y$も2倍、3倍…と同じく変化する関係のことをいいます。

$y=ax$において、

• $x=1$のとき$y=a$
• $x=2$のとき$y=2a$
• $x=3$のとき$y=3a$

と$x$と$y$が比例として説明される関係にあることがわかります。

　1次関数のグラフは直線となります。

$y=ax$のグラフを考えます。

$x=0$のとき$y=a\cdot0=0$なので、$y=ax$のグラフは$(0,0)$、すなわち原点$O$を通ります。

$x=1$における点$(1, a)$をとり、この点を$A$とします。

$x=p$（$p:0$以外の任意の実数）における点$(p, ap)$をとり、この点を$P$とします。

点$A,P$それぞれからx軸へ垂線をおろし、その足を$Q,R$とすると、それぞれの座標は$(1,0),(p,0)$となります。

$△OAQ$と$△OPR$に着目すると

• $OQ\perp AQ,OR\perp PR$より、$∠OQA=∠ORP=90°$
• $OQ=1,OR=|p|, AQ=|a|, PR=|ap|$より、$OQ:OR=AQ:PR=1:|p|$

2組の辺の長さの比とその間の角がそれぞれ等しいので$△OAQ$と$△OPR$は相似であることがわかります。
このことから$∠AOQ=∠POR$です。

ここで$p$が正であるときを考えると、$∠AOQ$と$∠POR$は共通の角となり、3点$O,A,P$は同一直線上にあります。
また、$p$が負であるときを考えると、$∠AOQ$と$∠POR$は対頂角となり、やはり3点$O,A,P$は同一直線上にあります。

$p$をどのようにとっても点$P$は2点$O,A$を通る直線上に存在するので、1次関数$y=ax$のグラフは原点を通る直線であることがわかります。

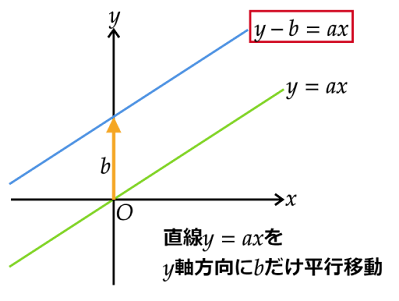
$y=ax+b$（ただし、$b\neq0$）のグラフは、$y=ax$と同様に考えることもできますが、グラフの平行移動で考えてみます。

1次関数$y=ax$のグラフをy軸方向に$b$だけ平行移動したあとの方程式は

$$y-b=ax$$

すなわち、$y$について解けば

$$y=ax+b$$

となります。

関連：関数のグラフの平行移動

平行移動前後でグラフの形は変わらないので、1次関数$y=ax+b$のグラフもまた直線であることがわかります。

また、1次関数$y=ax$と$y=ax+b$（ただし、$b\neq0$）のグラフは互いに平行移動した直線という関係なので、$a$が等しい1次関数のグラフは互いに平行であるといえます。

　1次関数$y=ax+b$において、$x=0$のとき$y=a\cdot0+b=b$、すなわちグラフ上の点$(0,b)$を表し、これは$y=ax+b$のグラフとy軸との交点です。
$b$は1次関数のグラフとy軸との交点のy座標に現れる数であり、y切片と呼ばれます。

同様に1次関数のグラフとx軸との交点のx座標に現れる数であるx切片もあります。

1次関数$y=ax+b$のグラフの右上がりや右下がりの度合いは$a$の値によって異なるため、$a$は傾きと呼ばれます。

直線の傾きは$x$が$1$増加したときの$y$の変化量によって評価できるので、変化の割合によって求めることができます。

関連：平均変化率とは？

1次関数$y=ax+b$において、$x$が$s$から$t$（$s,t:$任意の実数,$s<t$）まで変化したとき、$y$は$as+b$から$at+b$まで変化します。

このときの変化の割合は

$$\begin{align*}\frac{(at+b)-(as+b)}{t-s}&=\frac{at-as}{t-s}\\[0.5em]&=\frac{a(t-s)}{t-s}\\[0.5em]&=a\end{align*}$$

となり、傾き$a$と等しくなります。

1次関数$y=ax+b$のグラフは、$a>0$のときは右上がりの直線、$a<0$のときは右下がりの直線、1次関数ではなくなりますが$a=0$のときはx軸に平行な直線となります。