3つの外接する円の共通接線の交点と三角形の関係は？

「半径がそれぞれ$1,2,3$の円$\text{O$_1$, O$_2$, O$_3$}$が互いに外接している。
円$\text{O$_1$}$と$\text{O$_2$}$の接点$\text{Q}$を通る共通接線、円$\text{O$_2$}$と$\text{O$_3$}$の接点$\text{R}$を通る共通接線、円$\text{O$_3$}$と$\text{O$_1$}$の接点$\text{S}$を通る共通接線は点$\text{P}$で交わる。
このとき以下の問いに答えよ。

(1)各円の中心を頂点とする$△\text{O$_1$O$_2$O$_3$}$において点$\text{P}$はなんという点であるか？三角形に関係する点の名称で答えよ。

(2)$\text{PQ}$の長さを求めよ。」

このような問題はどのように解けばよいのでしょうか？

(1)

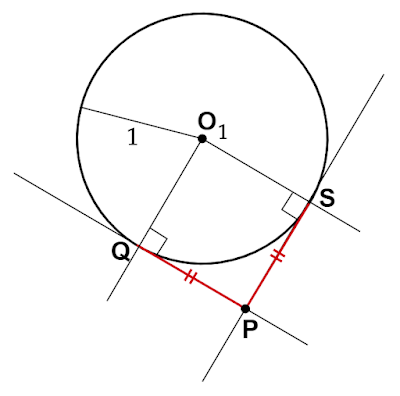
　円$\text{O$_1$}$と２本の接線$\text{PQ, PS}$に着目します。

接線$\text{PQ, PS}$はそれぞれ円$\text{O$_1$}$の半径$\text{O$_1$Q},\text{O$_1$S}$に対して垂直です。
また、円外の点からその点を通る2本の接線上の接点までの距離は等しくなるので$\text{PQ}=\text{PS}$となります。

関連：The two tangent theoreom（2接線の定理）

すなわち、円$\text{O$_1$}$と接線$\text{PQ, PS}$について

\[\text{O$_1$Q}⊥\text{PQ},\quad \text{O$_1$S}⊥\text{PS},\quad \text{PQ}=\text{PS}\]

が成り立つということです。

同様に円$\text{O$_2$}$と接線$\text{PQ, PR}$、円$\text{O$_3$}$と接線$\text{PR, PS}$についても言えるので

\begin{array}{c}\text{O$_2$Q}⊥\text{PQ},& \text{O$_2$R}⊥\text{PR},& \text{PQ}=\text{PR}\\[0.5em]\text{O$_3$R}⊥\text{PR},& \text{O$_3$S}⊥\text{PS},& \text{PR}=\text{PS}\end{array}

が成り立つことがわかります。

　以上をまとめると

\begin{array}{c}\text{O$_1$O$_2$}⊥\text{PQ},&\text{O$_2$O$_3$}⊥\text{PR},& \text{O$_3$O$_1$}⊥\text{PS}\\[0.5em]&\text{PQ}=\text{PR}=\text{PS}&\end{array}

となります。

これは、$\text{O$_1$O$_2$, O$_2$O$_3$, O$_3$O$_1$}$それぞれに対する垂線$\text{PQ, PR, PS}$の長さ、すなわち点$\text{P}$から$△\text{O$_1$O$_2$O$_3$}$の各辺までの距離が等しいということなので、点$\text{P}$は$△\text{O$_1$O$_2$O$_3$}$の内心であることがわかります。

関連：三角形の内心が角の二等分線の交点で求められるのはナゼ？

(2)

　円$\text{O$_1$, O$_2$, O$_3$}$の半径はそれぞれ$1,2,3$なので、$\text{O$_1$O$_2$}=3,\text{O$_2$O$_3$}=5,$ $\text{O$_3$O$_1$}=4$となります。
したがって、$△\text{O$_1$O$_2$O$_3$}$の面積はヘロンの公式より

\begin{align*}s&=\frac{\text{O$_1$O$_2$}+\text{O$_2$O$_3$}+\text{O$_3$O$_1$}}{2}\\[0.5em]&=\frac{3+5+4}{2}\\[0.5em]&=6\\[1em]△\text{O$_1$O$_2$O$_3$}&=\sqrt{s(s-\text{O$_1$O$_2$})(s-\text{O$_2$O$_3$})(s-\text{O$_3$O$_1$})}\\[0.5em]&=\sqrt{6\cdot3\cdot1\cdot2}\\[0.5em]&=6\end{align*}

となります。

関連：ヘロンの公式　三角形の3辺から面積を求める公式

また、$△\text{O$_1$O$_2$O$_3$}$の各頂点と内心$\text{P}$を線で結ぶと$△\text{PO$_1$O$_2$},△\text{PO$_2$O$_3$},△\text{PO$_3$O$_1$}$の3つに分割されます。

$△\text{O$_1$O$_2$O$_3$}$の各辺を底辺と考えるとこれらの三角形はそれぞれ$\text{PQ, PR, PS}$の長さを高さとし、(1)より$\text{PQ}=x$とおくと$\text{PQ}=\text{PR}=\text{PS}=x$となります。

　$△\text{PO$_1$O$_2$},△\text{PO$_2$O$_3$},△\text{PO$_3$O$_1$}$それぞれの面積の和が$△\text{O$_1$O$_2$O$_3$}$の面積となるので、ここから

\begin{align*}△\text{PO$_1$O$_2$}+△\text{PO$_2$O$_3$}+△\text{PO$_3$O$_1$}&=△\text{O$_1$O$_2$O$_3$}\\[0.5em]\frac{1}{2}\cdot3x+\frac{1}{2}\cdot5x+\frac{1}{2}\cdot4x&=6\\[0.5em]\frac{1}{2}(3x+5x+4x)&=6\\[0.5em]6x&=6\\[0.5em]x&=1\end{align*}

となり、$\text{PQ}$の長さは$1$であるとわかります。