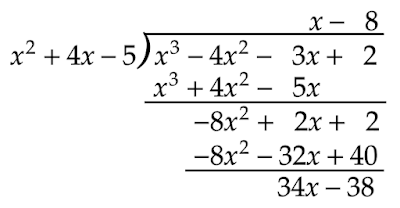「次の分数式を部分分数分解せよ。ただし、分解後の分数式の分子の次数は$0$になるようにすること。
(1)$\large\dfrac{4x-9}{2x^2-x-15}$
(2)$\large-\dfrac{4x}{(x+3)^2(3x+9)}$
(3)$\large\dfrac{x^3-4x^2-3x+2}{x^2+4x-5}$」このような問題はどのように解けばよいのでしょうか?
(1)$\tfrac{4x-9}{2x^2-x-15}$
一見部分分数分解できないように見えますが、分母が
\[2x^2-x-15=(2x+5)(x-3)\]
と因数分解できるので分解できます。
\[2x^2-x-15=(2x+5)(x-3)\]
と因数分解できるので分解できます。
このことから、部分分数分解したものは
両辺に$(2x+5)(x-3)$を掛けて分母を払うと
\begin{align*}\frac{4x-9}{2x^2-x-15}&=\frac{4x-9}{(2x+5)(x-3)}\\[0.5em]&=\frac{A}{2x+5}+\frac{B}{x-3}\tag{I}\end{align*}
とおけます。両辺に$(2x+5)(x-3)$を掛けて分母を払うと
\[4x-9=A(x-3)+B(2x+5)\]
となり、これは恒等式となります。
$A,B$を係数比較法で求めます。
右辺を展開して整理すると
右辺を展開して整理すると
\begin{align*}4x-9&=Ax-3A+2Bx+5B\\[0.5em]&=(A+2B)x+(-3A+5B)\end{align*}
両辺の係数を比較すると
\[\left\{\begin{aligned}A+2B&=4&\cdots\text{(i)}\\[1em]-3A+5B&=-9&\cdots\text{(ii)}\end{aligned}\right.\]
これを解くと、$\text{(i)}$より$A=4-2B\quad\cdots\text{(iii)}$
これを$\text{(ii)}$に代入して
\begin{align*}-3(4-2B)+5B&=-9\\[0.5em]-12+11B&=-9\\[0.5em]B&=\frac{3}{11}\end{align*}
$\text{(iii)}$より
\begin{align*}A&=4-2\times\frac{3}{11}\\[0.5em]&=\frac{38}{11}\end{align*}
したがって、$\text{(I)}$は
\begin{align*}\frac{4x-9}{2x^2-x-15}&=\cfrac{\cfrac{38}{11}}{2x+5}+\cfrac{\cfrac{3}{11}}{x-3}\\[0.5em]&=\frac{38}{11(2x+5)}+\frac{3}{11(x-3)}\\[0.5em]&\left\{=\frac{1}{11}\left(\frac{38}{2x+5}+\frac{3}{x-3}\right)\right\}\end{align*}
となります。
(2)$-\tfrac{4}{(x+3)^2(3x+9)}$
部分分数分解をすると、一見
分母の因数が互いに素ではない場合なので、分解したものは
\[-\frac{4x}{(x+3)^2(3x+9)}=\frac{Ax+B}{(x+3)^2}+\frac{C}{3x+9}\]
とおけそうですが、分母をよく見ると$3x+9=3(x+3)$なので
\[-\frac{4x}{(x+3)^2(3x+9)}=-\frac{4x}{3(x+3)^3}\]
と変形できます。分母の因数が互いに素ではない場合なので、分解したものは
\[-\frac{4x}{(x+3)^2(3x+9)}=\frac{A}{x+3}+\frac{B}{(x+3)^2}+\frac{C}{(x+3)^3}\tag{II}\]
とおけます。
両辺に$(x+3)^2(3x+9)=3(x+3)^3$を掛けて分母を払うと
$\text{(vi)}$より
\begin{align*}-4x&=3A(x+3)^2+3B(x+3)+3C\\[0.5em]&=3Ax^2+18Ax+27A+3Bx+9B+3C\\[0.5em]&=3Ax^2+3(6A+B)x+3(9A+3B+C)\end{align*}
両辺の係数を比較すると
\[\left\{\begin{aligned}3A&=0&\cdots\text{(iv)}\\[1em]3(6A+B)&=-4&\cdots\text{(v)}\\[1em]3(9A+3B+C)&=0&\cdots\text{(vi)}\end{aligned}\right.\]
これを解くと$\text{(iv)}$より$A=0$、これを$\text{(v)}$に代入して$B=-\dfrac{4}{3}$となるから
$\text{(vi)}$より
\begin{align*}9A+3B+C&=0\\[0.5em]9\cdot0+3\cdot\left(-\frac{4}{3}\right)+C&=0\\[0.5em]C&=4\end{align*}
したがって、$\text{(II)}$は
\begin{align*}-\frac{4x}{(x+3)^2(3x+9)}&=\frac{0}{x+3}+\cfrac{-\cfrac{4}{3}}{(x+3)^2}+\frac{4}{(x+3)^3}\\[0.5em]&=-\frac{4}{3(x+3)^2}+\frac{4}{(x+3)^3}\end{align*}
となります。
(3)$\tfrac{x^3-4x^2-3x+2}{x^2+4x-5}$
分母と分子それぞれの次数を比較すると、分子のほうが最高次数が大きくなっています。
\[\frac{x^3-4x^2-3x+2}{x^2+4x-5}=(x^3-4x^2-3x+2)÷(x^2+4x-5)\]
と書けるので、まずは整式の割り算をして分子の最高次数を下げます。
割り算の結果より
\[x^3-4x^2-3x+2=(x-8)(x^2+4x-5)+34x-38\]
と書けるので、両辺を$x^2+4x-5$で割ることで
\[\frac{x^3-4x^2-3x+2}{x^2+4x-5}=x-8+\frac{34x-38}{x^2+4x-5}\]
のように分子の最高次数を下げた形に変形することができます。
また、$x^2+4x-5=(x+5)(x-1)$と因数分解できることから、$\dfrac{34x-38}{x^2+4x-5}$を部分分数分解したものは
\[\frac{34x-38}{x^2+4x-5}=\frac{A}{x+5}+\frac{B}{x-1}\tag{III}\]
とおけます。
両辺に$x^2+4x-5=(x+5)(x-1)$を掛けて分母を払うと
\begin{align*}34x-38&=A(x-1)+B(x+5)\\[0.5em]&=Ax-A+Bx+5B\\[0.5em]&=(A+B)x+(-A+5B)\end{align*}
両辺の係数を比較すると
\[\left\{\begin{aligned}A+B&=34&\cdots\text{(vii)}\\[1em]-A+5B&=-38&\cdots\text{(viii)}\end{aligned}\right.\]
これを解くと$\text{(vii)}$より$A=34-B\quad\cdots\text{(ix)}$
これを$\text{(viii)}$に代入して
\begin{align*}34-B+5B&=-38\\[0.5em]4B&=-72\\[0.5em]B&=-18\end{align*}
$\text{(ix)}$より$A=52$
したがって、$\text{(III)}$は
\begin{align*}\frac{34x-38}{x^2+4x-5}&=\frac{52}{x+5}+\frac{-18}{x-1}\\[0.5em]&=\frac{52}{x+5}-\frac{18}{x-1}\end{align*}
となるので、問の分数式を部分分数分解したものは
\[\frac{x^3-4x^2-3x+2}{x^2+4x-5}=x-8+\frac{52}{x+5}-\frac{18}{x-1}\]
となります。
Share: