$10$の累乗の計算は指数関数の定義と指数の計算法則が基本となります。
累乗とは?
$10$の累乗$10^n$は$n$が自然数の場合、($1$に)$10$が$n$個掛け合わされていることを意味します。
ここでは説明を省きますが、$10^0$は$1$、$10^{-n}$は$10^n$の逆数を表します。
関連:0乗はなぜ1になる?
$10$の累乗は整数や小数で表すと位取りの$0$が指数の絶対値の個数分並びます。
指数の加減
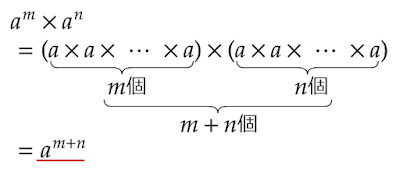
指数の計算法則により$10$の累乗同士の掛け算・割り算は指数の足し算・引き算になります。
例:
\begin{align*}10^6\times10^3&=10^{6+3}\\[0.5em]&=10^9\\[1.5em]0.01\times100000&=10^{-2}\times10^5\\[0.5em]&=10^{-2+5}\\[0.5em]&=10^3\\[1.5em]\frac{10^9}{10^{16}}&=10^{9-16}\\[0.5em]&=10^{-7}\\[1.5em]\frac{10^8}{100}&=\frac{10^8}{10^2}\\[0.5em]&=10^{8-2}\\[0.5em]&=10^{6}\end{align*}
これを利用して、$10$の累乗を分解することができます。
$10^n$は前述した通り$10$が$n$個掛けられている数です。
この$n$個の$10$を$m$個と$n-m$個に分解してそれぞれ累乗に直すと$10^m\times10^{n-m}$となります。
例:
\begin{align*}n=5,m=3\\ 10^5&=10^3\times10^{5-3}\\[0.5em]&=10^3\times10^2\end{align*}
$m$は$n$より大きい数や負の数にすることもできます。
例:
\begin{align*}n=5,m=8\\ 10^5&=10^8\times10^{5-8}\\[0.5em]&=10^8\times10^{-3}\\[0.5em]&=\frac{10^8}{10^3}\\[1.5em]n=8,m=-3\\ 10^8&=10^{-3}\times10^{8-(-3)}\\[0.5em]&=10^{-3}\times10^{11}\\[0.5em]&=\frac{10^{11}}{10^3}\end{align*}
こういった変形は$10$の累乗を含む項同士の和・差を求めるときに同類項を作るために利用されます。
例:
\begin{align*}1.2\times10^4+8.2\times10^3&=1.2\times10^4+8.2\times10^{-1}\times10^4\\[0.5em]&=1.2\times10^4+0.82\times10^4\\[0.5em]&=2.02\times10^4\end{align*}
指数の乗除
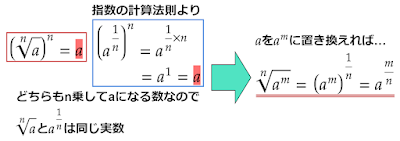
指数の計算法則により$10$の累乗の累乗は指数の掛け算、$10$の累乗の累乗根は指数の割り算となります。
累乗するものが2数の積のときは
\[(ab)^n=a^nb^n\]
を利用します。
指数の割り算を行わないときは根号の計算を利用して計算します。
\begin{align*}\sqrt[n]{ab}&=\sqrt[n]{a}\sqrt[n]{b}\\[0.5em]\sqrt[n]{a^n}&=a\\ ただし、nが偶数のときは\\ \sqrt[n]{a^n}&=|a|\end{align*}
例:
\begin{align*}(10^{-2})^2&=10^{-2\times2}\\[0.5em]&=10^{-4}\\[1.5em](2\times10^2)^6&=2^6\times10^{2\times6}\\[0.5em]&=64\times10^{12}\\[1.5em]\sqrt[3]{10^5}&=\sqrt[3]{10^3\times10^2}\\[0.5em]&=\sqrt[3]{10^3}\times\sqrt[3]{10^2}\\[0.5em]&=10\sqrt[3]{10^2}\\[1.5em]\sqrt{1.2\times10^3}&=\sqrt{12\times10^2}\\[0.5em]&=\sqrt{12}\times\sqrt{10^2}\\[0.5em]&=\sqrt{4\times3}\times|10|\\[0.5em]&=\sqrt{4}\times\sqrt{3}\times10\\[0.5em]&=2\times\sqrt{3}\times10\\[0.5em]&=20\sqrt{3}\\[1.5em]\left(\sqrt[3]{10}\right)^5&=\left(10^\frac{1}{3}\right)^5\\[0.5em]&=10^\frac{5}{3}\\[0.5em]&=10^{1+\frac{2}{3}}\\[0.5em]&=10\times10^\frac{2}{3}\\[0.5em]&=10\sqrt[3]{10^2}\end{align*}
関連:指数の計算法則
Share:
https://p-suugaku.blogspot.com/2022/12/10-ruijou.html10の累乗の計算
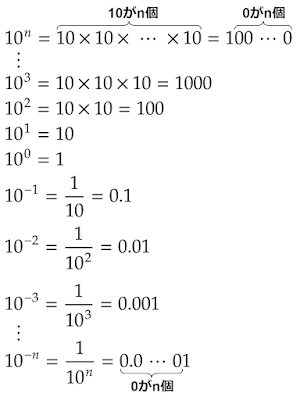
.png)
.png)
.png)