交わる2直線間を等しい長さの線分で分割したときの角度

「上図の(1)、(2)で示した角度$x, y$の大きさを求めよ。」

このような問題はどのように解けばよいのでしょうか？

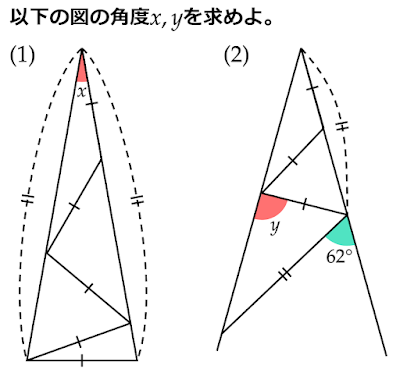
(1)

　まずは上図のようにアルファベットを振ります。

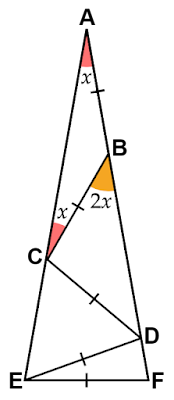
$△\text{ABC}$において$\text{BA}=\text{BC}$である二等辺三角形なので$∠\text{BAC}=∠\text{BCA}=x$となります。

また、外角の定理より

$$∠\text{CBD}=∠\text{BAC}+∠\text{BCA}=2x$$

となることがわかります。

次は$△\text{BCD}$において$\text{CB}=\text{CD}$である二等辺三角形なので$∠\text{CBD}=∠\text{CDB}=2x$となります。

$\text{BC}$の延長線$\text{CG}$を引くと、外角の定理より

$$∠\text{DCG}=∠\text{CBD}+∠\text{CDB}=4x$$

となります。

また、対頂角より$∠\text{BCA}=∠\text{GCE}=x$であるから

$$∠\text{DCE}=∠\text{DCG-}∠\text{GCE}=3x$$

となることがわかります。

$△\text{CDE}$においても$△\text{BCD}$と同様にして$∠\text{EDF}=4x$となることがわかります。

$△\text{DEF}$において$\text{ED}=\text{EF}$である二等辺三角形なので、$∠\text{EDF}=∠\text{EFD}=4x$となります。
また、$△\text{AEF}$は$\text{AE}=\text{AF}$である二等辺三角形なので、$∠\text{EFD}=∠\text{AEF}=4x$となります。

三角形の内角の和は$180°$であるから

$$\begin{align*}∠\text{BAC}+∠\text{EFD}+∠\text{AEF}&=180°\\[0.5em]x+4x+4x&=180°\\[0.5em]9x&=180°\\[0.5em]x&=20°\end{align*}$$

（※$∠\text{BAC}$は上図の$∠\text{DAE}$のこと）であるとわかります。

(2)

　上図のようにアルファベットを振り、$∠\text{BAC}=a$とおいて(1)と同様に角度を求めていくと、

$$y=4a-a=3a\tag{*}$$

となることがわかります。

また、$△\text{ADE}$において$\text{DA}=\text{DE}$である二等辺三角形なので、$∠\text{DAE}=∠\text{DEA}=a$となり、外角の定理より

$$\begin{align*}∠\text{EDF}&=∠\text{DAE}+∠\text{DEA}\\[0.5em]&=2a=62°\end{align*}$$

となります。

このことから$a=31°$であることがわかるため、$(*)$に代入して

$$y=3\times31°=93°$$

と求められます。

関連：外角の定理

関連：対頂角、同位角、錯角とは

関連：二等辺三角形の特徴