台形を対角線で分割したときにできる三角形の面積の性質

　台形を対角線で分割したときにできる三角形にはどのような性質があるでしょうか？

1本の対角線で分割してできる三角形

　台形を1本の対角線で分割すると2つの三角形ができます。
これらの三角形の面積比は$(\textbf{上底}):(\textbf{下底})$となります。

　$AB//CD$である台形$ABCD$を対角線$AC$で分割し、$△ABC$と$△ACD$をつくります。

$△ABC$において辺$AB$を底辺とすると、高さは頂点$C$から辺$AB$またはその延長へおろした垂線の長さとなります。
$△ABC$の高さを$h$とおくと、その面積は

$$\begin{equation}\triangle ABC=\frac{h}{2}\cdot AB\end{equation}$$

となります。

同様に、$△ACD$において辺$CD$を底辺とすると、高さは頂点$A$から辺$CD$またはその延長へおろした垂線の長さとなります。
$△ACD$の高さを$h'$とおくと、その面積は

$$\begin{equation}\triangle ACD=\frac{h'}{2}\cdot CD\end{equation}$$

となります。

ところで、台形$ABCD$の高さは底辺$AB,CD$いずれかの辺上の1点からもう一方の底辺またはその延長へおろした垂線の長さとなります。
すなわち、台形$ABCD$と$△ABC,△ACD$の高さは等しいということであり、$h=h'$が成り立ちます。
すると、$(1),(2)$はそれぞれ

$$\begin{align*}\triangle ABC&=\frac{h}{2}\cdot AB\tag*{(1)'}\\[1em]\triangle ACD&=\frac{h}{2}\cdot CD\tag*{(2)'}\end{align*}$$

と書けます。

したがって、$(1)',(2)'$より$△ABC$と$△ACD$の面積比は

$$\begin{align*}\triangle ABC:\triangle ACD&=\frac{h}{2}\cdot AB:\frac{h}{2}\cdot CD\\[0.5em]&=AB:CD\end{align*}$$

となり、上底$AB$と下底$CD$の長さの比に等しいことがわかります。これは対角線$BD$で分割した場合も同様です。

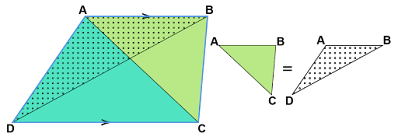
　$AB//CD$である台形$ABCD$において、1本の対角線で分割してできる三角形のうち辺$AB$を含む三角形は、対角線$AC$で分割したときの$△ABC$と対角線$BD$で分割したときの$△ABD$の2つがありますが、これらの面積は等しくなります。

　辺$AB$を$△ABC$と$△ABD$の底辺とすると、$△ABC$の高さは頂点$C$から辺$AB$またはその延長へおろした垂線の長さ、$△ABD$の高さは頂点$D$から辺$AB$またはその延長へおろした垂線の長さとなります。
上述より台形$ABCD$の高さと$△ABC,△ABD$の高さは等しいです。

したがって、$△ABC,△ABD$はともに底辺の長さと高さが等しいため面積が等しいことがわかります。

関連：三角形の等積変形

2本の対角線で分割してできる三角形

　台形を2本の対角線で分割すると4つの三角形ができます。
このうち台形の上底を含む三角形と下底を含む三角形は相似比が$(\textbf{上底}):(\textbf{下底})$の相似な三角形であり、面積比は$(\textbf{上底})^2:(\textbf{下底})^2$となります。

　$AB//CD$である台形$ABCD$の対角線$AC,BD$の交点を$P$とします。

$△PAB$と$△PCD$に着目すると

• $AB//CD$より錯角が等しいので$∠EAB=∠ECD$
• 同様に$∠EBA=∠EDC$
• 対頂角は等しいので$∠AEB=∠CED$

3組の角がそれぞれ等しいので相似であり、相似比は$AB:CD$であることがわかります。

相似な図形の面積比はその相似比の2乗に等しいので$AB^2:CD^2$となります。

関連：相似な三角形の面積比はなぜ相似比の2乗となるのか？

　台形を2本の対角線で分割してできた4つの三角形のうち、台形の脚を含む三角形の面積は等しくなります。

　$AB//CD$である台形$ABCD$の対角線$AC,BD$の交点を$P$とします。

$△PAD$と$△ABD,△PAB$の面積の関係に着目すると

$$\begin{equation}\triangle PAD=\triangle ABD-\triangle PAB\end{equation}$$

が成り立ちます。

また、$△PBC$と$△ABC,△PAB$の面積の関係に着目すると

$$\begin{equation}\triangle PBC=\triangle ABC-\triangle PAB\end{equation}$$

が成り立ちます。

ところで、$△ABD$と$△ABC$の面積は等しいです。
したがって、

$$\begin{align*}\triangle ABD&=\triangle ABC\\[0.5em]\triangle ABD-\triangle PAB&=\triangle ABC-\triangle PAB\\[0.5em]\triangle PAD&=\triangle PBC&\bigl(\because (3),(4)\bigr)\end{align*}$$

となり、台形$ABCD$を2本の対角線$AC,BD$で分割してできた4つの三角形のうち脚$AD$または$BC$を含む三角形$△PAD,△PBC$の面積が等しいことがわかります。

関連：台形とは？