「次の三角関数の値を求めよ。
(1)$\large\sin60°$
(2)$\large\cos135°$
(3)$\large\tan210°$」
(1)$\sin60°$
三角関数の値は直角三角形による三角関数の定義、または単位円による定義にしたがって求めます。$60°$は鋭角なのでどちらの定義でも求めることができます。
直角三角形による定義
$60°$の内角に着目すると、直角三角形による三角関数の定義より$\sin$の値は斜辺と対辺の長さの比なので
\begin{align*}\sin60°&=\frac{\text{BC}}{\text{CA}}\\[0.5em]&=\frac{\sqrt{3}}{2}\end{align*}
となります。
単位円による定義
.png)
なので、始線と$60°$の角をなす原点$\text{O}$を中心とする単位円の半径を考えます。この半径の円周上にある端点$\text{P}$からx軸へ垂線を下ろし、その足を$\text{Q}$とすると内角が$30°-60°-90°$の直角三角形$\text{OPQ}$ができます。
点$\text{P}$のy座標の絶対値はx軸へおろした垂線$\text{PQ}$の長さに等しいので、まずは垂線$\text{PQ}$の長さを求めます。
直角三角形$\text{OPQ}$は上の直角三角形$\text{ABC}$と相似なので3辺の比が$\text{OQ}:\text{PQ}:\text{OP}=1:\sqrt{3}:2$となります。
直角三角形$\text{OPQ}$の3辺の比と$\text{OP}=1$より
直角三角形$\text{OPQ}$は上の直角三角形$\text{ABC}$と相似なので3辺の比が$\text{OQ}:\text{PQ}:\text{OP}=1:\sqrt{3}:2$となります。
直角三角形$\text{OPQ}$の3辺の比と$\text{OP}=1$より
\begin{align*}\text{OP}:\text{PQ}&=2:\sqrt{3}\\[0.5em]1:\text{PQ}&=2:\sqrt{3}\\[0.5em]2\text{PQ}&=\sqrt{3}\\[0.5em]\text{PQ}&=\frac{\sqrt{3}}{2}\end{align*}
点$\text{P}$は第1象限にあるのでy座標は正。したがって
\begin{align*}\sin60°&=\text{PQ}\\[0.5em]&=\frac{\sqrt{3}}{2}\end{align*}
となります。
(2)$\cos135°$
$135°$は鈍角で直角三角形による定義ではあつかえない角度なので、単位円による定義で考えます。
$\cosθ$は始線と$θ$の角をなす原点を中心とする単位円の半径の円周上にある端点のx座標にあたります。
なので、始線と$135°$の角をなす原点$\text{O}$を中心とする単位円の半径を考えます。この半径の円周上にある端点$\text{P}$からx軸へ垂線を下ろし、その足を$\text{Q}$とするとx軸の負の部分と半径$\text{OP}$の間の角が$45°$であることから、内角が$45°-45°-90°$の直角三角形$\text{OPQ}$ができていることがわかります。
なので、始線と$135°$の角をなす原点$\text{O}$を中心とする単位円の半径を考えます。この半径の円周上にある端点$\text{P}$からx軸へ垂線を下ろし、その足を$\text{Q}$とするとx軸の負の部分と半径$\text{OP}$の間の角が$45°$であることから、内角が$45°-45°-90°$の直角三角形$\text{OPQ}$ができていることがわかります。
点$\text{P}$のx座標の絶対値は辺$\text{OQ}$の長さに等しいので、これを求めます。
直角三角形$\text{OPQ}$は上図左下の直角三角形$\text{ABC}$と相似なので3辺の比は$\text{OQ}:\text{PQ}:\text{OP}=1:1:\sqrt{2}$です。
直角三角形$\text{OPQ}$の3辺の比と$\text{OP}=1$より
直角三角形$\text{OPQ}$は上図左下の直角三角形$\text{ABC}$と相似なので3辺の比は$\text{OQ}:\text{PQ}:\text{OP}=1:1:\sqrt{2}$です。
直角三角形$\text{OPQ}$の3辺の比と$\text{OP}=1$より
\begin{align*}\text{OQ}:\text{OP}&=1:\sqrt{2}\\[0.5em]\text{OQ}:1&=1:\sqrt{2}\\[0.5em]\sqrt{2}\text{OQ}&=1\\[0.5em]\text{OQ}&=\frac{1}{\sqrt{2}}&\left(=\frac{\sqrt{2}}{2}\right)\end{align*}
点$\text{P}$は第2象限にあるのでx座標は負。したがって、
\begin{align*}\cos135°&=-\text{OQ}\\[0.5em]&=-\frac{1}{\sqrt{2}}&\left(=-\frac{\sqrt{2}}{2}\right)\end{align*}
となります。（三角関数の値は分母の有理化を行わなくても構いません。）
(3)$\tan210°$
$\tanθ$は始線と$θ$の角をなす原点を中心とする単位円の半径を延長した直線の傾き、あるいは半径の延長と直線$x=1$との交点のy座標にあたります。
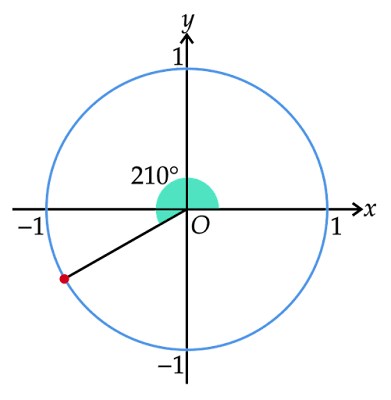
なので、まずは始線と$210°$の角をなす原点$\text{O}$を中心とする単位円の半径を考え、2通りの方法で求めてみます。
傾きから求める方法
.png)
半径の円周上の端点$\text{P}$からx軸へ垂線をおろし、その足を$\text{Q}$とします。
すると、x軸の負の部分と半径$\text{OP}$の間の角が30°であることから、内角が$30°-60°-90°$の直角三角形$\text{OPQ}$ができていることがわかります。
点$\text{P}$のx座標の絶対値は辺$\text{OQ}$の長さ、y座標の絶対値は辺$\text{PQ}$の長さに等しいので、これらを求めます。
直角三角形$\text{OPQ}$は上図左上の直角三角形$\text{ABC}$と相似なので3辺の比は$\text{OQ}:\text{PQ}:\text{OP}=\sqrt{3}:1:2$です。
直角三角形$\text{OPQ}$の3辺の比と$\text{OP}=1$より
直角三角形$\text{OPQ}$は上図左上の直角三角形$\text{ABC}$と相似なので3辺の比は$\text{OQ}:\text{PQ}:\text{OP}=\sqrt{3}:1:2$です。
直角三角形$\text{OPQ}$の3辺の比と$\text{OP}=1$より
\begin{align*}\text{OQ}:\text{OP}&=\sqrt{3}:2\\[0.5em]\text{OQ}:1&=\sqrt{3}:2\\[0.5em]2\text{OQ}&=\sqrt{3}\\[0.5em]\text{OQ}&=\frac{\sqrt{3}}{2}\\[1em]\text{PQ}:\text{OP}&=1:2\\[0.5em]\text{PQ}:1&=1:2\\[0.5em]2\text{PQ}&=1\\[0.5em]\text{PQ}&=\frac{1}{2}\end{align*}
点$\text{P}$は第3象限にあるのでx座標、y座標ともに負。したがって座標は$\left(-\dfrac{\sqrt{3}}{2},-\dfrac{1}{2}\right)$であることがわかります。
半径を延長した直線は原点と点$\text{P}$を通るので傾き$\tan210°$は
\begin{align*}\tan210°&=\frac{-\cfrac{1}{2}}{-\cfrac{\sqrt{3}}{2}}\\[0.5em]&=\frac{1}{\sqrt{3}}&\left(=\frac{\sqrt{3}}{3}\right)\end{align*}
となります。
交点のy座標から求める方法
.png)
点$\text{R}$のy座標の絶対値は辺$\text{RS}$の長さに等しいので、これを求めます。
x軸の負の部分と半径$\text{OP}$の間の角が$30°$であることから対頂角より$∠\text{ROS}=30°$なので、直角三角形$\text{ORS}$の内角は$30°-60°-90°$であることがわかります。
直角三角形$\text{ORS}$は上図右下の直角三角形$\text{ABC}$と相似なので、3辺の比は$\text{OS}:\text{RS}:\text{OR}=\sqrt{3}:1:2$です。
直角三角形$\text{ORS}$の3辺の比と$\text{OS}=1$より
x軸の負の部分と半径$\text{OP}$の間の角が$30°$であることから対頂角より$∠\text{ROS}=30°$なので、直角三角形$\text{ORS}$の内角は$30°-60°-90°$であることがわかります。
直角三角形$\text{ORS}$は上図右下の直角三角形$\text{ABC}$と相似なので、3辺の比は$\text{OS}:\text{RS}:\text{OR}=\sqrt{3}:1:2$です。
直角三角形$\text{ORS}$の3辺の比と$\text{OS}=1$より
\begin{align*}\text{OS}:\text{RS}&=\sqrt{3}:1\\[0.5em]1:\text{RS}&=\sqrt{3}:1\\[0.5em]\sqrt{3}\text{RS}&=1\\[0.5em]\text{RS}&=\frac{1}{\sqrt{3}}&\left(=\frac{\sqrt{3}}{3}\right)\end{align*}
点$\text{R}$は第1象限にあるのでy座標は正。したがって、
\begin{align*}\tan210°&=\text{RS}\\[0.5em]&=\frac{1}{\sqrt{3}}&\left(=\frac{\sqrt{3}}{3}\right)\end{align*}
となります。
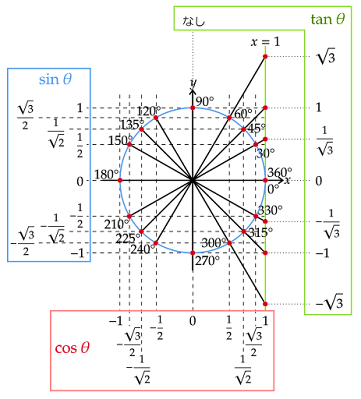
主な角度と三角関数の値は以下のようになります。
| 角度 | $\sin$ | $\cos$ | $\tan$ |
|---|---|---|---|
| $30°$ | $\dfrac{1}{2}$ | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{1}{\sqrt{3}}$ $ \small=\dfrac{\sqrt{3}}{3}$ |
| $45°$ | $\dfrac{1}{\sqrt{2}}$ $ \small=\dfrac{\sqrt{2}}{2}$ |
$\dfrac{1}{\sqrt{2}}$ $ \small=\dfrac{\sqrt{2}}{2}$ |
$1$ |
| $60°$ | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{1}{2}$ | $\sqrt{3}$ |
| $90°$ | $1$ | $0$ | なし |
| $120°$ | $\dfrac{\sqrt{3}}{2}$ | $-\dfrac{1}{2}$ | $-\sqrt{3}$ |
| $135°$ | $\dfrac{1}{\sqrt{2}}$ $ \small=\dfrac{\sqrt{2}}{2}$ |
$-\dfrac{1}{\sqrt{2}}$ $ \small=-\dfrac{\sqrt{2}}{2}$ |
$-1$ |
| $150°$ | $\dfrac{1}{2}$ | $-\dfrac{\sqrt{3}}{2}$ | $-\dfrac{1}{\sqrt{3}}$ $ \small=-\dfrac{\sqrt{3}}{3}$ |
| $180°$ | $0$ | $-1$ | $0$ |
| $210°$ | $-\dfrac{1}{2}$ | $-\dfrac{\sqrt{3}}{2}$ | $\dfrac{1}{\sqrt{3}}$ $ \small=\dfrac{\sqrt{3}}{3}$ |
| $225°$ | $-\dfrac{1}{\sqrt{2}}$ $ \small=-\dfrac{\sqrt{2}}{2}$ |
$-\dfrac{1}{\sqrt{2}}$ $ \small=-\dfrac{\sqrt{2}}{2}$ |
$1$ |
| $240°$ | $-\dfrac{\sqrt{3}}{2}$ | $-\dfrac{1}{2}$ | $\sqrt{3}$ |
| $270°$ | $-1$ | $0$ | なし |
| $300°$ | $-\dfrac{\sqrt{3}}{2}$ | $\dfrac{1}{2}$ | $-\sqrt{3}$ |
| $315°$ | $-\dfrac{1}{\sqrt{2}}$ $ \small=-\dfrac{\sqrt{2}}{2}$ |
$\dfrac{1}{\sqrt{2}}$ $ \small=\dfrac{\sqrt{2}}{2}$ |
$-1$ |
| $330°$ | $-\dfrac{1}{2}$ | $\dfrac{\sqrt{3}}{2}$ | $-\dfrac{1}{\sqrt{3}}$ $ \small=-\dfrac{\sqrt{3}}{3}$ |
| $360°$ | $0$ | $1$ | $0$ |
Share:
