二等辺三角形から30°-60°-90°の直角三角形の3辺の比が求まるまで

　二等辺三角形の性質を調べるところから始めて最終的に$30°-60°-90°$の直角三角形の3辺の比を求めてみます。
ただし、三角形の内角の和や三角形の合同、三平方の定理はすでにわかっているものとします。

二等辺三角形の性質

　二等辺三角形とは2辺の長さが等しい三角形のことです。
この三角形の性質を調べます。

$\text{AB}=\text{AC}$である二等辺三角形$\text{ABC}$の頂点$\text{A}$から底辺$\text{BC}$へ垂線をおろし、その足を$\text{D}$とすると、2つの直角三角形$△\text{ABD},△\text{ACD}$ができます。

$△\text{ABD}$と$△\text{ACD}$に着目すると、

• 共通の辺なので$\text{AD}=\text{AD}$
• 二等辺三角形の定義より$\text{AB}=\text{AC}$
• $\text{AD}\perp \text{BC}$より$∠\text{ADB}=∠\text{ADC}=90°$

直角三角形の斜辺と他の1辺がそれぞれ等しいので合同であることがわかります。

したがって、$\text{BD}=\text{CD}$、$∠\text{ABD}=∠\text{ACD}$、$∠\text{BAD}=∠\text{CAD}$が成り立ちます。
すなわち、以下のことがいえます。

1. 二等辺三角形の底辺の両端の角（底角）は等しい。
2. 二等辺三角形の頂点から底辺へおろした垂線は底辺の垂直二等分線かつ頂角の二等分線。

関連：二等辺三角形の特徴

正三角形の性質

　正三角形とは、二等辺三角形の1つで3辺の長さが等しい三角形のことです。
この三角形の性質を調べます。

正三角形$\text{ABC}$は、定義より$\text{AB}=\text{BC}=\text{CA}$です。
$\text{AB}=\text{CA}$であることに着目すると、
二等辺三角形の性質1.より$∠\text{BAC}=∠\text{BCA}(∠\text{ACB})\cdots(1)$

$\text{AB}=\text{BC}$であることに着目すると、
二等辺三角形の性質1.より$∠\text{ABC}=∠\text{ACB}\cdots(2)$

$(1),(2)$より$∠\text{ABC}=∠\text{BCA}=∠\text{CAB}(∠\text{BAC})$となり、3つの内角が等しいことがわかります。
そこで、それぞれの内角の大きさを$α$とおくと、三角形の内角の和は$180°$であることより

$$\begin{align*}∠\text{ABC}+∠\text{BCA}+∠\text{CAB}&=180°\\[0.5em]\alpha+\alpha+\alpha&=180°\\[0.5em]3\alpha&=180°\\[0.5em]\alpha&=60°\end{align*}$$

となり、以下のことがいえます。

正三角形の内角の大きさはすべて$60°$。

関連：頂角が$60°$の二等辺三角形が正三角形であることの証明

正三角形からできる直角三角形の性質

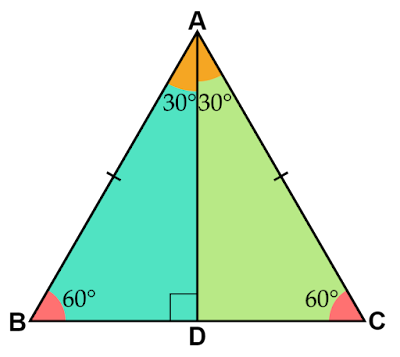
　正三角形の1つの頂点から対辺へおろした垂線で分割されてできる直角三角形の性質を調べます。

正三角形$\text{ABC}$の頂点$\text{A}$から対辺$\text{BC}$へ垂線をおろし、その足を$\text{D}$とすると2つの直角三角形$△\text{ABD},△\text{ACD}$ができます。

$△\text{ABD}$と$△\text{ACD}$に着目すると、

• 正三角形の性質より$∠\text{ABD}=∠\text{ACD}=60°$
• 二等辺三角形の性質2.と正三角形の性質より$\text{AD}$は$∠\text{BAC}=60°$の二等分線なので$∠\text{BAD}=∠\text{CAD}=30°$
• $\text{AD}\perp \text{BC}$より$∠\text{ADB}=∠\text{ADC}=90°$

であるので、$△\text{ABD},△\text{ACD}$はどちらも$30°-60°-90°$の直角三角形であることがわかります。

また、正三角形の定義より$\text{AB}=\text{BC}=\text{CA}$なので、各辺の長さを$a$とおき、
二等辺三角形の性質2.より$\text{AD}$は辺$\text{BC}$の垂直二等分線なので$\text{BD}=\text{CD}$であり、各線分の長さを$b$とおくと、$\text{BC}=\text{BD}+\text{CD}$より

$$\begin{align*}a&=b+b\\[0.5em]a&=2b\end{align*}$$

となります。

さらに、$△\text{ABD}$について三平方の定理より

$$\begin{align*}\text{AB}^2&=\text{AD}^2+\text{BD}^2\\[0.5em]a^2&=\text{AD}^2+b^2\\[0.5em](2b)^2&=\text{AD}^2+b^2\\[0.5em]4b^2&=\text{AD}^2+b^2\\[0.5em]\text{AD}^2&=3b^2\\[0.5em]\text{AD}&=\sqrt{3}b&(\because \text{AD}>0)\end{align*}$$

となるため、辺$\text{AD}$の長さは$\sqrt{3}b$であることがわかります。

関連：三平方の定理（ピタゴラスの定理）

すると、$30°-60°-90°$の直角三角形である$△\text{ABD}$の3辺の比は

$$\begin{align*}\text{AD}:\text{BD}:\text{AB}&=b:\sqrt{3}b:a\\[0.5em]&=b:\sqrt{3}b:2b\\[0.5em]&\large=1:\sqrt{3}:2\end{align*}$$

となることがわかります。