度数法と弧度法

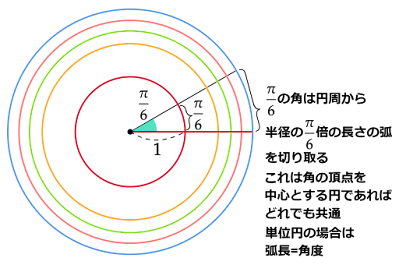
　度数法でも弧度法でも角の大きさを「その角が角の頂点を中心とする円の周からどれくらいの長さの弧を切り取るか」で表している点は共通しています。

しかし、「どれくらいの長さの弧」かを評価する基準が異なります。

度数法

　度数法は、切り取った弧の長さがもとの円周を$360$等分した弧何個分かで角の大きさを表す方法です。単位には度$[°]$をもちいます。

例えば、$10°$はその角が切り取った弧の長さが円周を$360$等分した弧$10$個分の長さとなるような角の大きさであることを意味します。

これは割合で考えると円周の$\dfrac{1}{360}$の弧の長さを基準として角がその何倍の長さの弧に切り取るかで角の大きさを表す方法であるということができます。

弧度法

　弧度法は、切り取った弧の長さがもとの円の半径を基準としてその何倍かで角の大きさを表す方法です。特に単位円の場合は半径が$1$なので弧長がそのまま弧度法における角度の値となります。単位にはラジアン$\text{[rad]}$をもちいます。

例えば、$\dfrac{\pi}{6}$ラジアンはその角が切り取った弧の長さが円の半径の$\dfrac{\pi}{6}$倍の長さとなるような角の大きさであることを意味します。単位円の場合はその角が切り取った弧の長さが$\dfrac{\pi}{6}$であるような角の大きさであることを意味します。

単位円の場合の弧の長さが$\dfrac{\pi}{6}$というのはどれくらいの長さなのかピンとこないですが、円周の長さが半径の$2\pi$倍、すなわち円周の長さは$2\pi$であることを考えれば、この弧の長さは円周の$\dfrac{1}{12}$であることがわかります。
また、$\dfrac{1}{12}=\dfrac{30}{360}$であることから度数法の$30°$に等しい大きさであることがわかります。

角度の変換

　度数法での角度と弧度法での角度は互いに変換することができます。

度数法での角度を$D\text{[°]}$、弧度法での角度を$R\text{[rad]}$、角の頂点を中心とする円の半径を$r$、角が円周から切り取った弧の長さを$l$とすると

度数法での角度は

$$D=\frac{l}{\cfrac{2\pi r}{360}}\tag{a}$$

によって求めることができます。基準となるもとの円の周を$360$等分した弧の長さは$\dfrac{2\pi r}{360}$の部分です。

弧度法での角度は

$$R=\frac{l}{r}\tag{b}$$

によって求めることができます。

ここで、$\text{(a)}$はより簡単にすることができ、

$$\begin{align*}D&=\frac{l}{\cfrac{\pi r}{180}}\\[0.5em]&=\frac{180l}{\pi r}\end{align*}$$

となり、更に変形して$\text{(b)}$より

$$\begin{align*}D&=\frac{l}{r}\cdot\frac{180}{\pi}\\[0.5em]&=R\frac{180}{\pi}\end{align*}$$

となります。

したがって、度数法での角度$D\text{[°]}$から弧度法での角度$R\text{[rad]}$へは

$$\large R=D\frac{\pi}{180}$$

で変換することができます。

弧度法での角度$R\text{[rad]}$から度数法での角度$D\text{[°]}$へは

$$\large D=R\frac{180}{\pi}$$

で変換することができます。

関連：一般角とは？