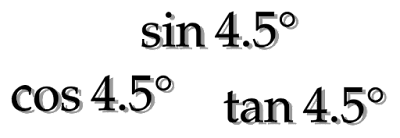$4.5°$ $(=\dfrac{\pi}{40})$のときの三角関数がどのような値となるのかを調べてみます。
$\sin4.5°$
$\sin$の加法定理より
\begin{align*}\sin4.5°&=\sin(22.5°-18°)\\[0.5em]&=\sin22.5°\cos18°-\cos22.5°\sin18°\end{align*}
となり、「$\sin22.5°,\cos22.5°,\tan22.5°$はどんな数?」、「$\sin18°,\cos18°,\tan18°$はどんな数?」より
\begin{align*}\sin22.5°&=\frac{\sqrt{2-\sqrt{2}}}{2}\\[0.5em]\cos22.5°&=\frac{\sqrt{2+\sqrt{2}}}{2}\\[1em]\sin18°&=\frac{\sqrt{5}-1}{4}\\[0.5em]\cos18°&=\frac{\sqrt{10+2\sqrt{5}}}{4}\end{align*}
なので
\begin{align*}\sin4.5°&=\frac{\sqrt{2-\sqrt{2}}}{2}\cdot\frac{\sqrt{10+2\sqrt{5}}}{4}-\frac{\sqrt{2+\sqrt{2}}}{2}\cdot\frac{\sqrt{5}-1}{4}\\[0.5em]&=\frac{\sqrt{20-10\sqrt{2}+4\sqrt{5}-2\sqrt{10}}}{8}-\frac{\sqrt{(2+\sqrt{2})(6-2\sqrt{5})}}{8}\\[0.5em]&=\frac{\sqrt{20-10\sqrt{2}+4\sqrt{5}-2\sqrt{10}}}{8}-\frac{\sqrt{12+6\sqrt{2}-4\sqrt{5}-2\sqrt{10}}}{8}\\[0.5em]&=\frac{\sqrt{20-10\sqrt{2}+4\sqrt{5}-2\sqrt{10}}-\sqrt{12+6\sqrt{2}-4\sqrt{5}-2\sqrt{10}}}{8}\\[0.5em]&\left(=\frac{\sqrt{2}\left(\sqrt{10-5\sqrt{2}+2\sqrt{5}-\sqrt{10}}-\sqrt{6+3\sqrt{2}-2\sqrt{5}-\sqrt{10}}\right)}{8}\right)\tag{a}\end{align*}
となります。
$\cos4.5°$
$\cos$の加法定理より
\begin{align*}\cos4.5°&=\cos(22.5°-18°)\\[0.5em]&=\cos22.5°\cos18°+\sin22.5°\sin18°\\[0.5em]&=\frac{\sqrt{2+\sqrt{2}}}{2}\cdot\frac{\sqrt{10+2\sqrt{5}}}{4}+\frac{\sqrt{2-\sqrt{2}}}{2}\cdot\frac{\sqrt{5}-1}{4}\\[0.5em]&=\frac{\sqrt{20+10\sqrt{2}+4\sqrt{5}+2\sqrt{10}}}{8}+\frac{\sqrt{(2-\sqrt{2})(6-2\sqrt{5})}}{8}\\[0.5em]&=\frac{\sqrt{20+10\sqrt{2}+4\sqrt{5}+2\sqrt{10}}}{8}+\frac{\sqrt{12-6\sqrt{2}-4\sqrt{5}+2\sqrt{10}}}{8}\\[0.5em]&=\frac{\sqrt{20+10\sqrt{2}+4\sqrt{5}+2\sqrt{10}}+\sqrt{12-6\sqrt{2}-4\sqrt{5}+2\sqrt{10}}}{8}\\[0.5em]&\left(=\frac{\sqrt{2}\left(\sqrt{10+5\sqrt{2}+2\sqrt{5}+\sqrt{10}}+\sqrt{6-3\sqrt{2}-2\sqrt{5}+\sqrt{10}}\right)}{8}\right)\tag{b}\end{align*}
となります。
$\tan4.5°$
三角関数の相互関係$\tanθ=\dfrac{\sinθ}{\cosθ}$と$\text{(a),(b)}$より
\begin{align*}\tan4.5°&=\frac{\sin4.5°}{\cos4.5°}\\[0.5em]&=\frac{\cfrac{\sqrt{2}\left(\sqrt{10-5\sqrt{2}+2\sqrt{5}-\sqrt{10}}-\sqrt{6+3\sqrt{2}-2\sqrt{5}-\sqrt{10}}\right)}{8}}{\cfrac{\sqrt{2}\left(\sqrt{10+5\sqrt{2}+2\sqrt{5}+\sqrt{10}}+\sqrt{6-3\sqrt{2}-2\sqrt{5}+\sqrt{10}}\right)}{8}}\\[0.5em]&=\frac{\sqrt{10-5\sqrt{2}+2\sqrt{5}-\sqrt{10}}-\sqrt{6+3\sqrt{2}-2\sqrt{5}-\sqrt{10}}}{\sqrt{10+5\sqrt{2}+2\sqrt{5}+\sqrt{10}}+\sqrt{6-3\sqrt{2}-2\sqrt{5}+\sqrt{10}}}\\[0.5em]&=\frac{\sqrt{(10+2\sqrt{5})-(5\sqrt{2}+\sqrt{10})}-\sqrt{(6-2\sqrt{5})+(3\sqrt{2}-\sqrt{10})}}{\sqrt{10+5\sqrt{2}+2\sqrt{5}+\sqrt{10}}+\sqrt{6-3\sqrt{2}-2\sqrt{5}+\sqrt{10}}}\\
&\qquad\cdot\frac{\sqrt{(10+2\sqrt{5})+(5\sqrt{2}+\sqrt{10})}-\sqrt{(6-2\sqrt{5})-(3\sqrt{2}-\sqrt{10})}}{\sqrt{10+5\sqrt{2}+2\sqrt{5}+\sqrt{10}}-\sqrt{6-3\sqrt{2}-2\sqrt{5}+\sqrt{10}}}\\[0.5em]&=\frac{\sqrt{60+20\sqrt{5}}-\sqrt{60-40\sqrt{2}-12\sqrt{5}+8\sqrt{10}}}{4(1+2\sqrt{2}+\sqrt{5})}\\
&\qquad+\frac{\sqrt{28-12\sqrt{5}}-\sqrt{60+40\sqrt{2}-12\sqrt{5}-8\sqrt{10}}}{4(1+2\sqrt{2}+\sqrt{5})}\\[0.5em]&=\frac{\sqrt{15+5\sqrt{5}}-\sqrt{15-10\sqrt{2}-3\sqrt{5}+2\sqrt{10}}}{2(1+2\sqrt{2}+\sqrt{5})}\\
&\qquad+\frac{\sqrt{7-3\sqrt{5}}-\sqrt{15+10\sqrt{2}-3\sqrt{5}-2\sqrt{10}}}{2(1+2\sqrt{2}+\sqrt{5})}\\[0.5em]&=\left(\frac{\sqrt{15+5\sqrt{5}}-\sqrt{15-10\sqrt{2}-3\sqrt{5}+2\sqrt{10}}}{2\bigl\{(1+\sqrt{5})+2\sqrt{2}\bigr\}}\right.\\
&\qquad\left.+\frac{\sqrt{7-3\sqrt{5}}-\sqrt{15+10\sqrt{2}-3\sqrt{5}-2\sqrt{10}}}{2\bigl\{(1+\sqrt{5})+2\sqrt{2}\bigr\}}\right)\cdot\frac{1+\sqrt{5}-2\sqrt{2}}{(1+\sqrt{5})-2\sqrt{2}}\\[0.5em]&=\frac{\sqrt{260-160\sqrt{2}+100\sqrt{5}-80\sqrt{10}}-\sqrt{180-120\sqrt{2}+52\sqrt{5}-40\sqrt{10}}}{4(\sqrt{5}-1)}\\
&\qquad+\frac{\sqrt{68+32\sqrt{2}-28\sqrt{5}-16\sqrt{10}}-\sqrt{180+120\sqrt{2}-76\sqrt{5}-56\sqrt{10}}}{4(\sqrt{5}-1)}\\[0.5em]&=\frac{\sqrt{65-40\sqrt{2}+25\sqrt{5}-20\sqrt{10}}-\sqrt{45-30\sqrt{2}+13\sqrt{5}-10\sqrt{10}}}{2(\sqrt{5}-1)}\\
&\qquad+\frac{\sqrt{17+8\sqrt{2}-7\sqrt{5}-2\sqrt{10}}-\sqrt{45+30\sqrt{2}-19\sqrt{5}-14\sqrt{10}}}{2(\sqrt{5}-1)}\\[0.5em]&=\left(\frac{\sqrt{65-40\sqrt{2}+25\sqrt{5}-20\sqrt{10}}-\sqrt{45-30\sqrt{2}+13\sqrt{5}-10\sqrt{10}}}{2(\sqrt{5}-1)}\right.\\
&\qquad\left.+\frac{\sqrt{17+8\sqrt{2}-7\sqrt{5}-2\sqrt{10}}-\sqrt{45+30\sqrt{2}-19\sqrt{5}-14\sqrt{10}}}{2(\sqrt{5}-1)}\right)\\
&\qquad\cdot\frac{\sqrt{5}+1}{\sqrt{5}+1}\\[0.5em]&=\frac{\sqrt{640-440\sqrt{2}+280\sqrt{5}-200\sqrt{10}}-\sqrt{400-280\sqrt{2}+168\sqrt{5}-120\sqrt{10}}}{8}\\
&\qquad+\frac{\sqrt{32+8\sqrt{2}-8\sqrt{5}-8\sqrt{10}}-\sqrt{80+40\sqrt{2}-24\sqrt{5}-24\sqrt{10}}}{8}\\[0.5em]&=\frac{\sqrt{160-110\sqrt{2}+70\sqrt{5}-50\sqrt{10}}-\sqrt{100-70\sqrt{2}+42\sqrt{5}-30\sqrt{10}}}{4}+\frac{\sqrt{8+2\sqrt{2}-2\sqrt{5}-2\sqrt{10}}-\sqrt{20+10\sqrt{2}-6\sqrt{5}-6\sqrt{10}}}{4}\end{align*}
となります。
それぞれの近似値は以下のようになります。
\begin{align*}\sin4.5°&=0.078459\\[1em]\cos4.5°&=0.99692\\[1em]\tan4.5°&=0.078702\end{align*}
Share: