三角関数を含む方程式（三角方程式）

「次の方程式を解け。右の括弧内を$θ$の範囲とする。

(1)$\large\cosθ=-\dfrac{\sqrt{2}}{2}$ $\large(0°\leqqθ<360°)$

(2)$\large\tanθ=\dfrac{\sqrt{3}}{3}$ $\large(0\leqqθ<2\pi)$

(3)$\large 2\sqrt{3}\sinθ+3=0$ $\large(0\leqqθ<2\pi)$

(4)$\large 2\cos^2θ=\cosθ$ $\large(500°\leqqθ\leqq1000°)$」

このような問題はどのように解けばよいでしょうか？

(1)$\cosθ=-\frac{\sqrt{2}}{2}$ $\large(0°\leqqθ<360°)$

　単位円による三角関数の定義に従って解きます。

関連：三角関数の読み方　②単位円の利用

単位円による定義より$\cosθ$はx軸の正の部分と反時計回りに$θ$の角をなす単位円の半径の円周上にある端点のx座標にあたります。

単位円周上の点のx座標が$-\dfrac{1}{2}$となるのは上図に示した第2象限と第3象限の2点が当てはまり、これらの点を通るそれぞれの単位円の半径が表す角度がこの方程式の解となります。

これらの点を通る直線$x=-\dfrac{\sqrt{2}}{2}$を引き、またそれぞれの点を通る半径も引きます。すると、半径、直線$x=-\dfrac{\sqrt{2}}{2}$、x軸で囲まれた直角三角形ができます。
どちらの直角三角形も斜辺は単位円の半径でもあるのでその長さは$1$、直線$x=-\dfrac{\sqrt{2}}{2}$上の辺の長さは各点のy座標の絶対値に等しいので$\dfrac{\sqrt{2}}{2}$です。すなわち斜辺と他の一辺がそれぞれ等しいので合同であることがわかります。したがって、原点を頂点とする内角の大きさをどちらも$\varphi$とおくことができます。

また、残る1辺の長さを$X$とおくと三平方の定理より

$$\begin{align*}\left(\frac{\sqrt{2}}{2}\right)^2+X^2&=1^2\\[0.5em]\frac{1}{2}+X^2&=1\\[0.5em]X^2&=\frac{1}{2}\\[0.5em]X&=\frac{\sqrt{2}}{2}&(\because X>0)\end{align*}$$

となるので、直角三角形の3辺の比は$\dfrac{\sqrt{2}}{2}:\dfrac{\sqrt{2}}{2}:1$、すなわち$1:1:\sqrt{2}$であることがわかります。

関連：三平方の定理（ピタゴラスの定理）

この3辺の比となる直角三角形は内角が$45°-45°-90°$の直角三角形で、$\varphi$にあたる内角は$45°$であることがわかります。

このことから第2象限にある点を通る半径が表す$0°\leqqθ<360°$を満たす角度は

$$\begin{align*}180°-\varphi&=180°-45°\\[0.5em]&=135°\end{align*}$$

第3象限にある点を通る半径が表す$0°\leqqθ<360°$を満たす角度は

$$\begin{align*}180°+\varphi&=180°+45°\\[0.5em]&=225°\end{align*}$$

です。

これらが方程式を満たす$θ$であるので

$$\theta=135°,225°$$

となります。

(2)$\tanθ=\frac{\sqrt{3}}{3}$ $(0\leqqθ<2\pi)$

　$(1)$と同様に解きます。

単位円による定義より$\tanθ$はx軸の正の部分と反時計回りに$θ$の角をなす単位円の半径を延長した直線の傾きであり、半径の延長と直線$x=1$との交点のy座標にもあたります。

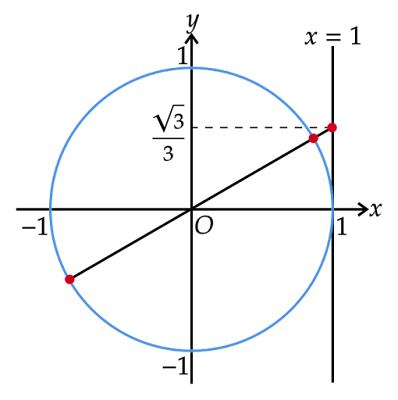
半径の延長と直線$x=1$との交点のy座標が$\dfrac{\sqrt{3}}{3}$となるのは、上図に示した第1象限の点を通る半径または第3象限の点を通る半径を延長したときであり、それぞれの半径が表す角度がこの方程式の解となります。

第1象限の点を通る半径または第3象限の点を通る半径を延長した直線はともに原点と$\left(1,\dfrac{\sqrt{3}}{3}\right)$を通るので同一の直線であることがわかります。したがって、第1象限の点を通る半径の表す角度を$\varphi$とおくと、第3象限の点を通る半径とx軸の間の角の大きさも対頂角なので$\varphi$となります。

半径とその延長、直線$x=1$、x軸で囲まれた直角三角形について考えると、x軸上の辺の長さが$1$、直線$x=1$上の辺の長さが$\dfrac{\sqrt{3}}{3}$です。
半径とその延長でもある辺の長さを$X$とおくと三平方の定理より

$$\begin{align*}X^2&=1^2+\left(\frac{\sqrt{3}}{3}\right)^2\\[0.5em]&=1+\frac{1}{3}\\[0.5em]&=\frac{4}{3}\\[0.5em]X&=\frac{2\sqrt{3}}{3}&(\because X>0)\end{align*}$$

となるので、直角三角形の3辺の比は$\dfrac{\sqrt{3}}{3}:1:\dfrac{2\sqrt{3}}{3}$、すなわち$1:\sqrt{3}:2$であることがわかります。

この3辺の比となる直角三角形は内角が$\dfrac{\pi}{6}-\dfrac{\pi}{3}-\dfrac{\pi}{2}$ $(30°-60°-90°)$の直角三角形で、$\varphi$にあたる内角は$\dfrac{\pi}{6}$であることがわかります。

このことから第1象限にある点を通る半径が表す$0\leqqθ<2\pi$を満たす角度は

$$\varphi=\frac{\pi}{6}$$

第3象限にある点を通る半径が表す$0\leqqθ<2\pi$を満たす角度は

$$\begin{align*}180°+\varphi&=\pi+\frac{\pi}{6}\\[0.5em]&=\frac{7}{6}\pi\end{align*}$$

です。

これらが方程式を満たす$θ$であるので

$$\theta=\frac{\pi}{6},\frac{7}{6}\pi$$

となります。

(3)$2\sqrt{3}\sinθ+3=0$ $(0\leqqθ<2\pi)$

　$\sinθ$についての1次方程式として解きます。

$$\begin{align*}2\sqrt{3}\sin\theta+3&=0\\[0.5em] 2\sqrt{3}\sin\theta&=-3\\[0.5em]\sin\theta&=-\frac{3}{2\sqrt{3}}\\[0.5em]&=-\frac{\sqrt{3}}{2}\end{align*}$$

　次に単位円による三角関数の定義に従って解きます。

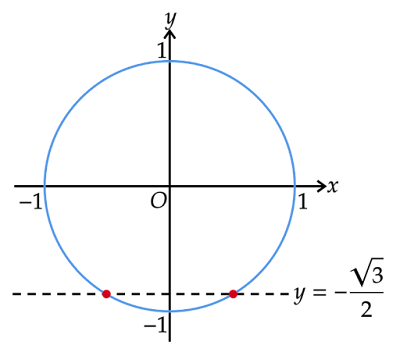
単位円による三角関数の定義より$\sinθ$はx軸の正の部分と反時計回りに$θ$の角をなす単位円の半径の円周上にある端点のy座標にあたります。

y座標が$-\dfrac{\sqrt{3}}{2}$となる点は上図に示した第3象限の点と第4象限の点の2つが当てはまり、これらの点を通るそれぞれの半径の表す角度がこの方程式の解となります。

これらの点からx軸へ垂線をおろし、またこれらの点を通る半径を引きます。すると半径、垂線、x軸に囲まれた直角三角形ができます。
どちらの直角三角形も斜辺は単位円の半径でもあるので長さが$1$、x軸へおろした垂線でもある辺の長さは各点のy座標の絶対値に等しいので$\dfrac{\sqrt{3}}{2}$です。すなわち、斜辺と他の1辺がそれぞれ等しいので合同であることがわかります。したがって、原点を頂点とする内角の大きさをどちらも$\varphi$とおくことができます。

三平方の定理よりもう1辺の長さを$X$として求めると

$$\begin{align*}1^2&=\left(\frac{\sqrt{3}}{2}\right)^2+X^2\\[0.5em]1&=\frac{3}{4}+X^2\\[0.5em]X^2&=\frac{1}{4}\\[0.5em]X&=\frac{1}{2}&(\because X>0)\end{align*}$$

となります。

したがって、直角三角形の3辺の比は$\dfrac{1}{2}:\dfrac{\sqrt{3}}{2}:1=1:\sqrt{3}:2$であることがわかります。この3辺の比となる直角三角形は内角が$\dfrac{\pi}{6}-\dfrac{\pi}{3}-\dfrac{\pi}{2}$ $(30°-60°-90°)$の直角三角形で、$\varphi$にあたる内角は$\dfrac{\pi}{3}$であることがわかります。

このことから、第3象限にある点を通る半径の表す角度は

$$\begin{align*}\varphi+\pi&=\frac{\pi}{3}+\pi\\[0.5em]&=\frac{4}{3}\pi\end{align*}$$

第4象限にある点を通る半径の表す角度は

$$\begin{align*}2\pi-\varphi&=2\pi-\frac{\pi}{3}\\[0.5em]&=\frac{5}{3}\pi\end{align*}$$

です。

これらが方程式を満たす$θ$であるので

$$\theta=\frac{4}{3}\pi,\frac{5}{3}\pi$$

となります。

(4)$2\cos^2θ=\cosθ$ $(500°\leqqθ\leqq1000°)$

　$\cosθ=x$とおき、2次方程式として解きます。

$$\begin{align*}2x^2&=x\\ 2x^2-x&=0\\[0.5em]x(2x-1)&=0\\[0.5em]x&=0,\frac{1}{2}\end{align*}$$

したがって、

$$\cos\theta=0,\frac{1}{2}$$

まずは$\cosθ=0$について考えます。

$\cosθ=0$となるのは上図に示した単位円とy軸との交点である2点が当てはまります。
これらの点を通る半径の表す角度は$0°\leqqθ\leqq360°$においては$θ=90°,270°$です。
しかし、求める$θ$の範囲は$0°\leqqθ\leqq360°$の範囲外なので$θ=90°,270°$をもちいて一般角でこれらの点を通る半径の表す角度を考えるとそれぞれ$θ=90°+360°×n,$$270°+360°×n$ （$n$：整数）と書けます。

$\cosθ=\dfrac{1}{2}$について考えると上図に示した単位円上の第1象限の点と第4象限の点の2点が当てはまります。
$(1)$と同様にして、これらの点を通る半径の表す角度は$0°\leqqθ\leqq360°$においては$θ=60°,300°$であることがわかります。
こちらも$θ=60°,300°$をもちいて一般角でこれらの点を通る半径の表す角度を考えるとそれぞれ$θ=60°+360°×n,$$300°+360°×n$ （$n$：整数）と書けます。

　それぞれの一般角表記の$θ$から範囲内であるものを絞り込みます。

$$\begin{align*}500°&=140°+360°\times1\\[1em]1000°&=280°+360°\times2\end{align*}$$

なので$θ$の範囲は$140°+360°×1\leqqθ\leqq280°+360°×2$と書くことができます。

$360°$に掛けられている数は一般角表記の$θ$の$n$にあたる部分なので、求める$θ$は少なくとも$n=1,2$を代入したものに限られることがわかります。

それぞれの一般角表記の$θ$に$n=1,2$を代入すると

$$\theta=\begin{array}{r}60°+360°\times 1,&60°+360°\times 2,\\[0.5em]90°+360°\times 1,&90°+360°\times 2,\\[0.5em]270°+360°\times 1,&270°+360°\times 2,\\[0.5em]300°+360°\times 1,&300°+360°\times 2.\end{array}$$

この中で範囲内にあるものは

$$\theta=\begin{array}{r}270°+360°\times 1,&300°+360°\times 1,&\\[0.5em]60°+360°\times 2,&90°+360°\times 2,&270°+360°\times 2.\end{array}$$

すなわち

$$\theta=630°,660°,780°,810°,990°$$

となり、これらが求める$θ$です。

(2024/2)問題の追加＆内容を修正しました。

関連：度数法と弧度法

関連：定義にしたがって三角関数の値を求める

関連：三角関数を含む不等式を解く