長さの測れないコンパスで長さの等しい線分を作図するには

「$\text{A, B, C}$の3つの点がある。コンパスと定規で$\text{AD}=\text{BC}$となるような点$\text{D}$を作図せよ。ただし、コンパスは針が紙面から離れたとき必ず閉じなければならない。」

このような問題はどのように解けばよいでしょうか？

　コンパスの使用に特に制限がなければ平行四辺形を作ったり、上図のように線分$\text{BC}$の長さをコンパスで測って点$\text{A}$を中心とする円を描いて円周上の任意の点を$\text{D}$とすれば良いのですが、「コンパスは針が紙面から離れたとき必ず閉じなければならない。」があるためこれらの方法は使えません。

したがって、コンパスを使用する際は長さを測った時点でその場で円を描かなければならないことになります。

　この問題を解く方法には以下の2通りがあります。

その1

1.

線分$\text{AB}$の垂直二等分線を作図します。

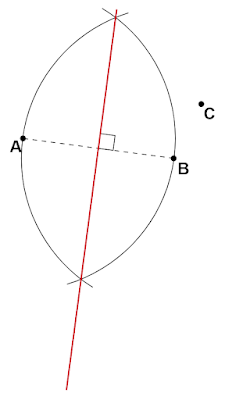
$\text{AB}$の長さを半径とする円弧を点$\text{A, B}$それぞれを中心として描き、2つの交点を結ぶ直線を引きます。

2.

半直線$\text{CB}$を引き、$\text{AB}$の垂直二等分線との交点を$\text{P}$とします。

3.

$\text{CP}$を半径とする円弧を描きます。

4.

半直線$\text{PA}$を引き、3.の円弧との交点を$\text{D}$とします。

以上で$\text{AD}=\text{BC}$となる点$\text{D}$を作図することができました。

解説

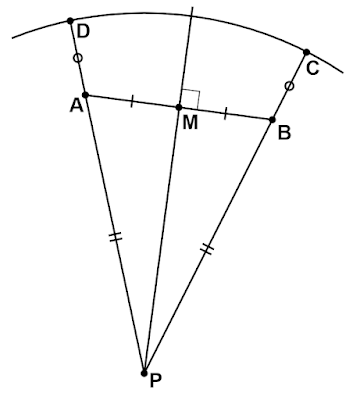
　線分$\text{BC}$をある直線に関して対称移動して点$\text{A}$が$\text{B}$へ移動したとすると、点$\text{D}$が$\text{C}$の移動先となります。このとき対称軸となる直線は線分$\text{AB}$の垂直二等分線となります。また、同時に線分$\text{CD}$の垂直二等分線でもあります。

垂直二等分線の性質より、垂直二等分線上の一点を点$\text{P}$とすると$\text{AP}=\text{BP, CP}=\text{DP}$が成り立ちます。

関連：垂直二等分線上の点以外に等距離の点は存在する？

また、線分$\text{AD}$と線分$\text{BC}$が線対称な位置関係にあるのならば、これらを延長した直線$\text{AD}$と直線$\text{BC}$も線対称な位置関係にあり、その交点は垂直二等分線上となります。
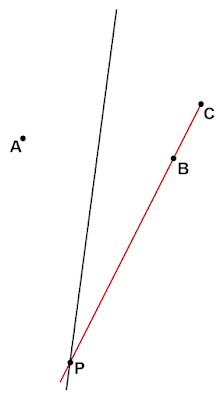
したがって、点$\text{P}$を垂直二等分線と直線$\text{BC}$との交点とすれば、直線$\text{AP}$上の$\text{CP}=\text{DP}$を満たし点$\text{C}$と線対称な位置関係である点が点$\text{D}$となります。

また、$\text{DP}=\text{AP}+\text{AD, CP}=\text{BP}+\text{BC}$であることを利用すれば、$\text{AD}$の長さは

\begin{align*}\text{CP}&=\text{DP}\\[0.5em]\text{BP}+\text{BC}&=\text{AP}+\text{AD}\\[0.5em]\text{AP}+\text{BC}&=\text{AP}+\text{AD}&(\because \text{AP}=\text{BP})\\[0.5em]\text{BC}&=\text{AD}\end{align*}

となり、問題の条件を満たしていることがわかります。

その2

1.

線分$\text{AB}$の垂直二等分線を作図します。

2.

線分$\text{BC}$の垂直二等分線を作図し、$\text{AB}$の垂直二等分線との交点を$\text{P}$とします。

3.

$\text{AP}$を半径とする円弧を描きます。

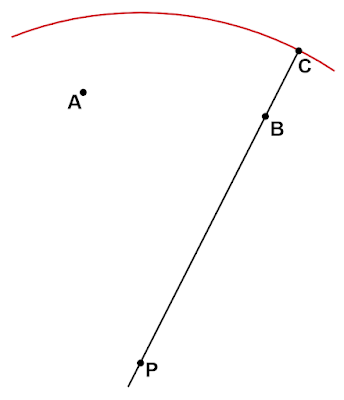
これは$△\text{ABC}$の外接円なので、$\text{AP}=\text{BP}=\text{CP}$が成り立ちます。

4.

$\text{AB}$の垂直二等分線上に任意の点$\text{Q}$をとり、これを中心とする点$\text{C}$を通る円弧を描きます。

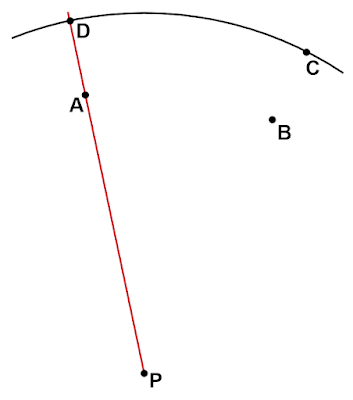
3.の円弧との点$\text{C}$以外の交点を$\text{D}$とします。

以上で$\text{AD}=\text{BC}$となる点$\text{D}$を作図することができました。

解説

　こちらは円の弦の性質を利用しています。

点$\text{C}$と$\text{D}$が線対称な位置関係にあるのならば、線分$\text{CD}$の垂直二等分線が対称軸となります。

そして、点$\text{C, D}$が同一円周上にあるならば、線分$\text{CD}$の垂直二等分線上にその円の中心が存在します。

関連：円の弦の垂直二等分線と中心

線分$\text{CD}$は円$\text{P}$の弦であり円$\text{Q}$の弦でもある

線分$\text{CD}$の垂直二等分線と線分$\text{AB}$の垂直二等分線は同一の直線なので、この直線上の異なる2点$\text{P, Q}$をそれぞれ中心とし、点$\text{C}$を通る円を描けば点$\text{C}$以外の2円の交点が点$\text{D}$となります。

$\text{AD}=\text{BC}$を確かに満たしていることは以下のように確かめることができます。

　$△\text{ABC}$と$△\text{BAD}$に着目すると
共通の辺なので$\text{AB}=\text{BA}\ \cdots(1)$
円周角の定理より$∠\text{ACB}=∠\text{BDA}\ \cdots(2)$

点$\text{C, D}$は円$\text{P}$と円$\text{Q}$の交点なので$\text{CD}⊥\text{PQ}\ \cdots(3)$
直線$\text{PQ}$は線分$\text{AB}$の垂直二等分線なので$\text{AB}⊥\text{PQ}\ \cdots(4)$
$(3), (4)$より$\text{AB}//\text{CD}$

平行線の錯角は等しいので$∠\text{ACD}=∠\text{BAC}\ \cdots(5)$
円周角の定理より$∠\text{ACD}=∠\text{ABD}\ \cdots(6)$
$(5), (6)$より$∠\text{BAC}=∠\text{ABD}\ \cdots(7)$

$(1), (2), (7)$より1組の辺とその両端の角がそれぞれ等しいので$△\text{ABC}$と$△\text{BAD}$は合同であり、このことから$\text{BC}=\text{AD}$であることがわかります。

$\text{AB}$の垂直二等分線ではなく$\text{AC}$の垂直二等分線を作図した場合、以降同様の手順で別の位置に$\text{AD}=\text{BC}$を満たす点$\text{D}$を作図することができます。