中点連結定理の逆は成り立つ？

　中点連結定理は三角形のものと台形のものがありますが、それぞれの定理の逆は成り立つでしょうか？

三角形の中点連結定理の逆

　三角形の中点連結定理とは

「$△\text{ABC}$の2辺$\text{AB, AC}$それぞれの中点$\text{M, N}$を結んだ線分$\text{MN}$は辺$\text{BC}$と平行でその辺の長さの半分の長さをもつ」

という定理です。

これは以下のように書き換えることができます。
「$△\text{ABC}$の辺$\text{AB}$上の点$\text{M}$と辺$\text{AC}$上の点$\text{N}$について、点$\text{M, N}$が各辺の中点ならば線分$\text{MN}$は辺$\text{BC}$と平行でその辺との長さの関係は$\text{BC}=2\text{MN}$である。」

すると、三角形の中点連結定理の逆は
「$△\text{ABC}$の辺$\text{AB}$上の点$\text{M}$と辺$\text{AC}$上の点$\text{N}$について、辺$\text{BC}$と平行でその辺との長さの関係が$\text{BC}=2\text{MN}$ならば、点$\text{M, N}$はそれぞれ辺$\text{AB, AC}$の中点である。」
となります。
これが成り立つことを確かめます。

　線分$\text{MN}$の$\text{N}$の側を延長し、$\text{MN}=\text{ND}$となるように点$\text{D}$をとります。
したがって、$\text{MD}=\text{BC}$です。

四角形$\text{BCDM}$に着目すると$\text{BC}//\text{MD, BC}=\text{MD}$より1組の対辺が平行、かつ長さが等しいので平行四辺形であることがわかります。
このことから

\begin{align}\text{BM}&//\text{CD}\\[0.5em]\text{BM}&=\text{CD}\end{align}

が成り立ちます。

　$△\text{AMN}$と$△\text{CDN}$に着目すると

上記より$\text{MN}=\text{DN}$
対頂角は等しいので$∠\text{ANM}=∠\text{CND}$
$(1)$より錯角は等しいので$∠\text{AMN}=∠\text{CDN}$

1組の辺とその両端の角がそれぞれ等しいので合同であることがわかります。

このことから

\begin{align}\text{AM}&=\text{CD}\\[0.5em]\text{AN}&=\text{CN}\end{align}

です。

$(2), (3)$より

\begin{equation}\text{AM}=\text{BM}\end{equation}

$(4), (5)$より2点$\text{M, N}$はそれぞれ辺$\text{AB, AC}$の中点であることがわかるので、三角形の中点連結定理の逆が成り立つことがわかります。

台形の中点連結定理の逆

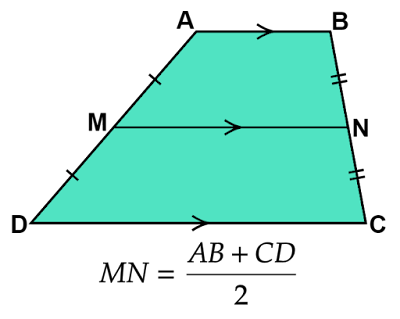
　台形の中点連結定理とは

「$\text{AB}//\text{CD}$である台形$\text{ABCD}$の平行でない対辺$\text{AD, BC}$それぞれの中点$\text{M, N}$を結んだ線分$\text{MN}$は辺$\text{AB, CD}$に平行で、その長さは$\dfrac{\text{AB}+\text{CD}}{2}$である。」

という定理です。

これは以下のように書き換えることができます。
「$\text{AB}//\text{CD}$である台形$\text{ABCD}$の平行でない対辺$\text{AD, BC}$のそれぞれに端点$\text{M, N}$をもつ線分$\text{MN}$について、端点が各辺の中点ならば線分$\text{MN}$は辺$\text{AB, CD}$に平行でその長さは$\text{MN}=\dfrac{\text{AB}+\text{CD}}{2}$である。」

すると、台形の中点連結定理の逆は
「$\text{AB}//\text{CD}$である台形$\text{ABCD}$の平行でない対辺$\text{AD, BC}$のそれぞれに端点$\text{M, N}$をもつ線分$\text{MN}$について、辺$\text{AB, CD}$に平行でその長さは$\text{MN}=\dfrac{\text{AB}+\text{CD}}{2}$ならば2点$\text{M, N}$はそれぞれ辺$\text{AD, BC}$の中点である。」
となります。
これが成り立つことを確かめます。

　台形$\text{ABCD}$の上底$\text{AB}$の長さを$a$、下底$\text{CD}$の長さを$b$とする（$a<b$とします）と、線分$\text{MN}$の長さは$\dfrac{a+b}{2}$となります。

辺$\text{AD}$に平行で点$\text{B}$を通る直線を引き、線分$\text{MN}$との交点を$\text{E}$、辺$\text{CD}$との交点を$\text{F}$とします。

四角形$\text{ABEM, MEFD}$に着目すると、$\text{AB}//\text{ME}//\text{DF}$かつ$\text{AD}//\text{BF}$より2組の対辺がそれぞれ平行なので、すべて平行四辺形であることがわかります。
このことから

\begin{align}\text{AB}&=\text{ME}=\text{DF}=a\\[0.5em]\text{AM}&=\text{BE}\\[0.5em]\text{MD}&=\text{EF}\end{align}

です。
$(6)$より

\begin{align*}\text{EN}&=\text{MN-ME}\\[0.5em]&=\frac{a+b}{2}-a\\[0.5em]&=\frac{b-a}{2}\\[1em]\text{CF}&=\text{CD-DF}\\[0.5em]&=b-a\end{align*}

です。

ここで$△\text{BCF}$に着目すると$\text{CF}//\text{EN, CF}=2\text{EN}$より三角形の中点連結定理の逆より

\begin{align}\text{BN}&=\text{CN}\\[0.5em]\text{BE}&=\text{EF}\end{align}

が成り立ちます。
また、$(7), (8), (10)$より

\begin{equation}\text{AM}=\text{DM}\end{equation}

であることがわかります。

$(9), (11)$より点$\text{M, N}$はそれぞれ辺$\text{AD, BC}$の中点であることがわかり、台形の中点連結定理の逆が成り立つことがわかります。

　以上より三角形と台形、どちらの中点連結定理の逆も成り立つことを確かめることができました。

関連：三角形と台形の中点連結定理