高低差からテーブルの高さを求める

「テーブル1脚とそれぞれ高さが異なる3個の花瓶A、B、Cがある。花瓶を2個選び、1つをテーブルを設置した床の上に、もう1つをテーブルの上に置いて2つの花瓶の頭頂部の高低差を調べると以下のようになった。

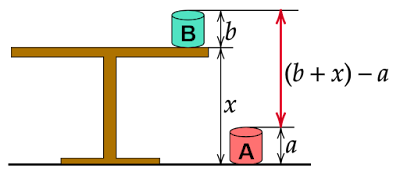
1. 花瓶Aを床に、花瓶Bをテーブルの上に置いたときの花瓶A、Bの高低差は$46$cm。
2. 花瓶Bを床に、花瓶Cをテーブルの上に置いたときの花瓶B、Cの高低差は$58$cm$。
3. 花瓶Cを床に、花瓶Aをテーブルの上に置いたときの花瓶A、Cの高低差は$40$cm。

このときのテーブルの高さを求めよ。ただし、テーブルの高さはどの花瓶よりも高いものとする。 また、花瓶A、B、Cの高さの合計が$42$cmのとき各花瓶の高さを求めよ。」

　テーブルの高さを$x$[cm]、花瓶A、B、Cの高さをそれぞれ$a,b,c$[cm]として式をつくります。

1.の場合

　床に置いた花瓶Aの高さは$a$[cm]、テーブルに置いた花瓶Bの高さは$b+x$[cm]です。
すると花瓶A、Bの高低差は$(b+x)-a$となるので等式は

$$\begin{equation}(b+x)-a=46\end{equation}$$

となります。

2.の場合

　床に置いた花瓶Bの高さは$b$[cm]、テーブルに置いた花瓶Cの高さは$c+x$[cm]です。
すると花瓶B、Cの高低差は$(c+x)-b$となるので等式は

$$\begin{equation}(c+x)-b=58\end{equation}$$

となります。

3.の場合

　床に置いた花瓶Cの高さは$c$[cm]、テーブルに置いた花瓶Aの高さは$a+x$[cm]です。
すると花瓶A、Cの高低差は$(a+x)-c$となるので等式は

$$\begin{equation}(a+x)-c=40\end{equation}$$

となります。

テーブルの高さを求める

　$(1),(2),(3)$から$x$を求めます。

$(1)+(2)+(3)$より

$$\begin{align*}\bigl\{(b+x)-a\bigr\}+\bigl\{(c+x)-b\bigr\}&+\bigl\{(a+x)-c\bigr\}=46+58+40\\[0.75em]3x&=144\\[0.5em]x&=48\end{align*}$$

となるので、テーブルの高さは$48$cmであるとわかります。

各花瓶の高さを求める

　テーブルの高さがわかったので、$(1),(3)$の式それぞれの$x$に代入して変形します。

$$\begin{align*}(1):&\\ &&(b+48)-a&=46\\[0.5em]&&b&=a-2\tag*{(1)'}\\[1em](3):&\\ &&(a+48)-c&=40\\[0.5em]&&-c&=-a-8\\[0.5em]&&c&=a+8\tag*{(3)'}\end{align*}$$

また、花瓶A、B、Cの高さの合計が$42$cmなので

$$\begin{equation}a+b+c=42\end{equation}$$

$(4)$に$(1)',(3)'$を代入すると

$$\begin{align*}a+(a-2)+(a+8)&=42\\[0.5em]3a+6&=42\\[0.5em]3a&=36\\[0.5em]a&=12\end{align*}$$

となります。

これを$(1)',(3)'$に代入すると

$$\begin{align*}(1)':&\\ &&b&=12-2\\[0.5em]&&&=10\\[1em](3)':&\\ &&c&=12+8\\[0.5em]&&&=20\end{align*}$$

となります。

したがって、花瓶Aの高さは$12\text{[cm]}$、花瓶Bの高さは$10\text{[cm]}$、花瓶Cの高さは$20\text{[cm]}$であるとわかります。

　ちなみに4つの不明な数を4つの式から求めるこの問題は

$$\begin{cases}(b+x)-a=46\\[0.5em](c+x)-b=58\\[0.5em](a+x)-c=40\\[0.5em]a+b+c=42\end{cases}$$

という4つの式からなる連立方程式を解く問題であるといえます。

関連：連立方程式を解く