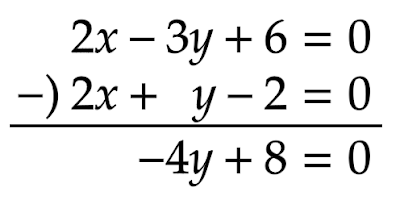「直線$l:2x-3y+6=0,m:2x+y-2=0$の交点と点$(3,7)$を通る直線の方程式を求めよ。」
このような問題はどのように解けばよいでしょうか?
直線$l$と$m$の交点は連立方程式によって求めることができます。連立方程式は
\[\left\{\begin{array}2x-3y+6&=0&\cdots\text{(a)}\\[0.5em]2x+y-2&=0&\cdots\text{(b)}\end{array}\right.\]
となります。
この連立方程式を解いて直線の方程式を求める方法と解かずに求める方法で問題を解いてみます。
1. 連立方程式を解く
$\text{(a)-(b)}$を計算すると
となるので$y$について解くと
\begin{align*}-4y+8&=0\\[0.5em]-4y&=-8\\[0.5em]y&=2\end{align*}
となります。これを$\text{(a)}$に代入すると
\begin{align*}2x-3\cdot2-6&=0\\[0.5em]2x&=0\\[0.5em]x&=0\end{align*}
となるので、交点の座標は$(0,2)$であるとわかります。
求める直線は$(0,2),\
(3,7)$の2点を通るので、2点を通る直線の方程式を求める公式
\begin{align*}(a_1,b_1),(a_2,b_2)&を通る直線の方程式は\\
y&=\frac{b_2-b_1}{a_2-a_1}(x-a_1)+b_1\end{align*}
より、
\begin{align*}y&=\frac{7-2}{3-0}(x-0)+2\\[0.5em]y&=\frac{5}{3}x+2\end{align*}
と求めることができます。
直線$l,m$と同様に一般形で書けば
\begin{align*}y&=\frac{5}{3}x+2\\[0.5em]3y&=5x+6\\[0.5em]5x-3y+6&=0\end{align*}
となります。
2. 連立方程式を解かない
実数$k$をもちいて$\text{(a)}+k\text{(b)}$を計算すると
(1.で求めた直線$l,m$の交点の座標$(0,2)$を代入すれば成り立つことから、確かに少なくとも直線$l,m$の交点を通る直線の方程式であることがわかります。)
\[(2x-3y+6)+k(2x+y-2)=0\]
となります。整理すれば
\[(2+2k)x-(3-k)y+6-2k=0\]
となり、直線の方程式の形になります。(1.で求めた直線$l,m$の交点の座標$(0,2)$を代入すれば成り立つことから、確かに少なくとも直線$l,m$の交点を通る直線の方程式であることがわかります。)
また、点$(3,7)$を通れば求める直線の方程式となるため$x=3,y=7$を代入して$k$の値を求めます。
\begin{align*}(2\cdot3-3\cdot7+6)+k(2\cdot3+7-2)&=0\\[0.5em]-9+11k&=0\\[0.5em]k&=\frac{9}{11}\end{align*}
したがって、求める直線の方程式は
1.と同様に一般形で書けば
\begin{align*}\left(2+2\cdot\frac{9}{11}\right)x-\left(3-\frac{9}{11}\right)y+6-2\cdot\frac{9}{11}&=0\\[0.5em]\frac{40}{11}x-\frac{24}{11}y+\frac{48}{11}&=0\\
\\
40x-24y+48&=0\\[0.5em]-24y&=-40x-48\\[0.5em]y&=\frac{5}{3}x+2\end{align*}
となります。
1.と同様に一般形で書けば
\[5x-3y+6=0\]
となります。
Share: