極限の不定形（∞-∞、0×∞）はなぜ極限値を出すことができないのか？

$$\Large\lim_{x\to\infty}(x-x^2)$$
　この極限はどうなるでしょうか？
このまま極限を計算しようとすると$x\to\infty$のとき$x^2\to\infty$なので、
$$\lim_{x\to\infty}(x-x^2)=\infty-\infty$$
となります。これは一例ですが$\infty-\infty$は不定形と呼ばれるもので、この状態では極限値を求めることはできません。

なぜ$\infty-\infty=0$としてはいけないのでしょうか？

　まず極限とはなにか？について考えます。
$$\lim_{x\to a}f(x)=b$$
とは”$x$が限りなく$a$に近づいたとき、$f(x)$は$b$に近づく”と説明されます。
「限りなく」とか「近づく」という言葉が使われています。これは極限が、ある値だけを代入するのではなく、ある値の周辺の値を代入してみてその変化からある値のときにどんな値になるのかを考えるものだからです。

　このことから不定形が極限値を出せない理由を考えてみます。

$$\lim_{x\to\infty}x^2$$
について考えます。
この極限は"$x$が限りなく大きくなったら$x^2$は何に近づく？"を意味していることになります。
なので、$x$にどんどん大きな値を代入していき、$x^2$の変化を見てみます。
$$\begin{align*}x=100\\ x^2&=100^2=10000\\ \\ x=1000\\ x^2&=1000^2=1000000\\ \\ x=10000\\ x^2&=10000^2=100000000\\ \\ &\vdots\end{align*}$$
このように$x$の値が大きくなるにつれて$x^2$のとる値も大きくなっていきます。
この場合、$x^2$の値は1つに定まらないため極限値は持たないものの、限りなく大きくなるため正の無限大に発散し、
$$\lim_{x\to\infty}x^2=\infty$$
のように書くことができます。

　同様にして$\lim_{x\to\infty}(x-x^2)$について考えます。
$$\begin{align*}x=100\\ x-x^2&=100-10000=-9900\\ \\ x=1000\\ x-x^2&=1000-1000000=-999000\\ \\ x=10000\\ x-x^2&=10000-100000000=-99990000\\ \\ &\vdots\end{align*}$$
$0$に近づくどころかどんどん小さくなっていきます。これは$x$が$1$より大きいとき$x^2$はより大きく増加するためです。（下図参照）

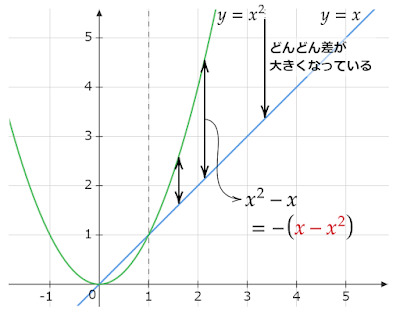図　グラフで見る$x$と$x^2$の増加量の違い

このように$x$が変化する過程に着目すると同じ$\infty$の記号であっても必ずしも両方が同じ値を持ちながら変化しているとは限りません。こういったことから不定形の状態でどんな極限値を持つのか判断できないということになります。

極限値を求めるには不定形を解消する必要があります。$x-x^2$の場合は因数分解します。

$$\begin{align*}\lim_{x\to\infty}(x-x^2)&=\lim_{x\to\infty}x(1-x)\\ \\ &=\infty\cdot(-\infty)&(\because x\to\inftyのとき1-x\to-\infty)\\ \\ &=-\infty\end{align*}$$

このように不定形を解消して負の無限大に発散することがわかります。

　他の不定形の例も見てみます。

$$\Large\lim_{x\to0}\frac{x^2}{x}$$

このまま極限値を求めようとすると

$$\lim_{x\to0}\frac{x^2}{x}=\frac{0}{0}$$

となります。あるいは分解して考えて

$$\begin{align*}\lim_{x\to0}\frac{x^2}{x}&=\lim_{x\to0}\left(x^2\cdot\frac{1}{x}\right)\\ \\ &=0\cdot\infty\end{align*}$$

とも書けます。

$\dfrac{0}{0},\ 0\cdot\infty$も不定形なので極限値を出すことができません。

$\dfrac{0}{0}$は計算できない形なので良いとして、$0\cdot\infty$は$0$となるように思われます。

不定形を解消するために約分をして極限値を求めます。

$$\begin{align*}\lim_{x\to0}\frac{x^2}{x}&=\lim_{x\to0}x\\ \\ &=0\end{align*}$$

このように不定形を解消すれば極限値が$0$になることがわかります。

上記よりやはり$0\cdot\infty=0$は正しいのでは？と思うかもしれません。
しかし、
$$\Large\lim_{x\to0}\frac{x}{x}$$
という極限を考えたとき、
$$\begin{align*}\lim_{x\to0}\frac{x}{x}&=\lim_{x\to0}\left(x\cdot\frac{1}{x}\right)\\ \\ &=0\cdot\infty\end{align*}$$
とすれば同じ不定形となりますが、不定形を解消すると
$$\begin{align*}\lim_{x\to0}\frac{x}{x}&=\lim_{x\to0}1\\ \\ &=1\end{align*}$$
となり、必ずしも$0\cdot\infty=0$とはならないことがわかります。
したがって、$0\cdot\infty$も不定形であることがわかります。