ヴィヴィアーニの定理の拡張についての考察

　Wikipediaのヴィヴィアーニの定理のページにて正多角形と等角多角形、凸な等辺多角形においても成り立つとの記述があったので、このヴィヴィアーニの定理の拡張を自分なりに考察してみました。

四角形については以前の記事で言及しているので五角形をもちいます。

1. 正多角形の場合

1-1. 正多角形の内部の点の場合

　正多角形の場合、ここでは正五角形ABCDEで考えます。
正五角形ABCDEの内部の任意の場所に点Pをおき、点Pから辺CD、DE、EA、AB、BCそれぞれにおろした垂線の長さを$a,b,c,d,e$とします。

すると、点Pと各辺によってできる三角形PCD、PDE、PEA、PAB、PBCの面積の和は正五角形ABCDEの面積$S$となるから
\[S=△PCD+△PDE+△PEA+△PAB+△PBC\]

ここで、正五角形ABCDEの一辺の長さを$l$とすれば
\[S=\frac{1}{2}(a+b+c+d+e)l\]
となるので、垂線の長さの和は
\[a+b+c+d+e=\frac{2S}{l}\]
となり、点Pの位置に関わらず一定となります。

これは他の正多角形でも同様に面積を利用して示すことができるため、ヴィヴィアーニの定理は正多角形においても成り立つことがわかります。

1-2. 正多角形の外部の点の場合

　点Pが正五角形ABCDEの外部にある場合を考えます。

例えば上図のような位置に点Pがあった場合、△PAB、△PBC、△PCDのはみ出した部分は△PDE、△PEAと重なるので正五角形ABCDEの面積$S$は
\[S=△PAB+△PBC+△PCD-△PDE-△PEA\]
となります。

1-1.と同様に両辺を1辺の長さ$l$で割って整理すれば
\[a+b+c-d-e=\frac{2S}{l}\]
となります。

このことから垂線の長さの和は一定とはなりませんが、正多角形の外部にある三角形の垂線の長さを他の垂線の長さの和から引けば点Pが内部にあるときと同じ値で一定となることがわかります。

これは後述の等角多角形の場合で利用します。

2. 等辺多角形の場合

　等辺多角形には凸多角形と凹多角形の2の場合があります。

　凸な等辺多角形の場合、正多角形と同様に垂線の長さの和が一定となります。

上図のように等辺五角形ABCDEの内部の任意の場所に点Pをおけば

\[S=△PCD+△PDE+△PEA+△PAB+△PBC\]

という関係が成り立ち、等辺五角形ABCDEの1辺の長さ$l$で割って整理すれば

\[a+b+c+d+e=\frac{2S}{l}\]

となり、これは一定となります。

したがって、凸な等辺多角形においてヴィヴィアーニの定理が成り立つことがわかります。

凹部のある等辺多角形の場合、点Pの位置によっては多角形からはみ出るように三角形ができるときがあり、上図の場合△PBCのはみ出した部分の面積は△PABの面積を差し引くことで打ち消すことができ、他の3つの三角形の面積を加えれば等辺五角形ABCDEの面積$S$なので

\[S=-△PAB+△PBC+△PCD+△PDE+△PEA\]

等辺五角形ABCDEの1辺の長さ$l$で割って整理すれば

\[-a+b+c+d+e=\frac{2S}{l}\]

となるので、凹部のある等辺多角形では必ずしも垂線の長さの和が一定となるわけではないことがわかります。

　以上より、等辺多角形においてヴィヴィアーニの定理が成り立つのは凸な等辺多角形であるときのみであることがわかります。

3. 等角多角形の場合

　等角多角形は頂点の数が等しいある正多角形と比較するとすべての対応する辺が平行であるので、正多角形の辺を平行移動したものが等角多角形であるといえます。

これを利用して等角多角形におけるヴィヴィアーニの定理を考えます。

3-1. 点Pが等角多角形と正多角形の内部にある場合

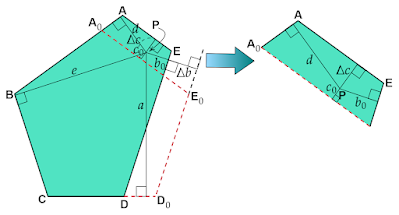
　点Pが等角五角形ABCDEの内部にあり、かつ正五角形$A_0BCD_0E_0$の内部にある場合を考えます。

上図の正五角形$A_0BCD_0E_0$において点Pから辺CD、DE、EA、AB、BCにひいた垂線の長さを$a_0,b_0,c_0,d_0,e_0$とします。
等角五角形ABCDEは正五角形$A_0BCD_0E_0$を変形したものであるとすると、辺$D_0E_0$と$E_0A_0$が平行移動しているからその移動量をそれぞれ$\Delta b, \Delta c$とし、正五角形$A_0BCD_0E_0$の外部への移動を正、内部への移動を負とします。

すると等角五角形ABCDEにおいて点Pから各辺へひいた垂線の長さの和は正五角形$A_0BCD_0E_0$の各辺へ引いた垂線の和に平行移動量を加えたものとなるため

\[a+b+c+d+e=a+(b_0+\Delta b)+(c_0+\Delta c)+d+e\]

となります。一般化すると

\begin{align*}&a+b+c+d+e\\ &=(a_0+\Delta a)+(b_0+\Delta b)+(c_0+\Delta c)+(d_0+\Delta d)+(e_0+\Delta e)\end{align*}

となります。

$a_0+b_0+c_0+d_0+e_0=k,\ \Delta a+\Delta b+\Delta c+\Delta d+\Delta e=\Delta k$は一定であるためこれらの和もまた一定となります。

3-2. 点Pが等角多角形の内部、正多角形の外部にある場合

　点Pが等角五角形ABCDEの内部にあり、正五角形$A_0BCD_0E_0$の外部にある場合を考えます。

正多角形の外部に点Pがある場合でも1-2.と同様に考えれば$c_0$だけを引けば点Pが内部にあるときの垂線の長さの和と値が等しくなるから、その値を$k$とすれば

\[a+b_0-c_0+d+e=k\]

となり、点Pのある場所の条件から$c_0<\Delta c$であるから

\[a+b+c+d+e=a+(b_0+\Delta b)+(\Delta c-c_0)+d+e=k+\Delta k\]

となり、垂線の長さの和は一定となります。

　3-1.、3-2.より等角多角形の任意の内部の点から各辺におろした垂線の長さの和は一定となります。

　以上よりヴィヴィアーニの定理は正多角形、凸な等辺多角形、等角多角形においても成り立つことがわかります。

関連：ヴィヴィアーニの定理

外部リンク：ヴィヴィアーニの定理 - Wikipedia