「pならばq」を否定すると？

　「$p$ならば$q$」という命題を否定すると何になるのでしょうか？

　「$p$ならば$q$」が真のときを考えます。

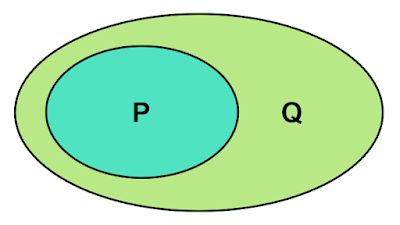「$p$ならば$q$」が真のとき

「$p$ならば$q$」が真のとき、必要条件、十分条件の関係をベン図で考えると上図のようになります。
$P$は条件$p$を満たす集合、$Q$は条件$q$を満たす集合です。（※全体集合$U$は省略）

「$p$ならば$q$」が真であるとは、集合$Q$の中の一部分が集合$P$であるということなので、これの否定とは「$p$ならば$q$」が偽、すなわち集合$P$の一部または全部が集合$Q$の外にあるということです。

「$p$ならば$q$」が偽のとき

では、そのことをどのように書けばよいかというと、集合$P$が集合$Q$の外にあることを指摘すればよいのです。

集合$P$の集合$Q$の外にある部分は集合$P$と集合$Q$の補集合$\overline{Q}$の重なり合っている部分なので$P\cap\overline{Q}$（$P$かつ$Q$でない）となります。これが「$p$ならば$q$」が真のときの否定となります。

「$p$ならば$q$」が真のとき「$P$かつ$Q$でない」部分はないので偽に、「$p$ならば$q$」が偽のとき「$P$かつ$Q$でない」部分があるので真となります。

「$P$かつ$Q$でない」は命題の真偽判定のときの反例が該当します。
例えば、「$x+y$が偶数ならば$x,y$ともに偶数である」は偽でその反例は「$x,y$ともに奇数」ですが、これは$P$にあたる「$x+y$が偶数」を満たしますが$Q$にあたる「$x,y$ともに偶数である」を満たさないので「$P$かつ$Q$でない」になっています。

　今度は「$P$かつ$Q$でない」の否定について考えてみます。

「$p$ならば$q$」が偽のとき

「$P$かつ$Q$でない」とは、上図のように集合$P$の一部または全部が集合$Q$の外にある部分のことなので、その否定とは集合$P$が集合$Q$の外にないということです。

$P\cap\overline{Q}$（$P$かつ$Q$でない）がないことは言い換えれば$P\cap\overline{Q}$（$P$かつ$Q$でない）でないことがどこでも成り立つことを意味します。

どこでも「$P$でない、または$Q$」が成り立つ

「$P$かつ$Q$でない」があると「$P$でない、または$Q$」でない部分になる

ド・モルガンの法則より$P\cap\overline{Q}$（$P$かつ$Q$でない）の否定は

$$\overline{P\cap\overline{Q}}=\overline{P}\cup Q$$
「$P$でない、または$Q$」となります。これが「$P$かつ$Q$でない」の否定となります。
また、「$p$ならば$q$」の否定（「$P$かつ$Q$でない」）の否定なので「$p$ならば$q$」と「$P$でない、または$Q$」は同値となります。