合成関数の最大値・最小値を求める

「次の関数の[ ]内の定義域における最大値と最小値を求めよ。
(1)

$$\begin{align*}y=(x^2-2x-3)^2+3(x^2-2x-3)+3\\ [1\leqq x\leqq3]&\end{align*}$$

(2)

$$\begin{align*}y=(x^2+4x-3)^3-(x^2+4x-3)^2-(x^2+4x-3)+2\\ [0\leqq x\leqq1]&\end{align*}$$

」

このような問題はどのように解けばよいでしょうか？

　これらはどんな関数が合成されているのかがわかりやすいので、まずは2つの関数に分解して考えます。

(1)

$x^2-2x-3=t$とおくと

$$\begin{align*}y&=t^2+3t+3\tag{a}\\[1em]t&=x^2-2x-3\tag{b}\end{align*}$$

という2つの関数に分解できます。
$\text{(a),(b)}$ともに2次関数なので平方完成すると

$$\begin{align*}y&=\left(t+\frac{3}{2}\right)^2+\frac{3}{4}\tag{c}\\[1em]t&=(x-1)^2-4\tag{d}\end{align*}$$

となります。

関連：平方完成するには

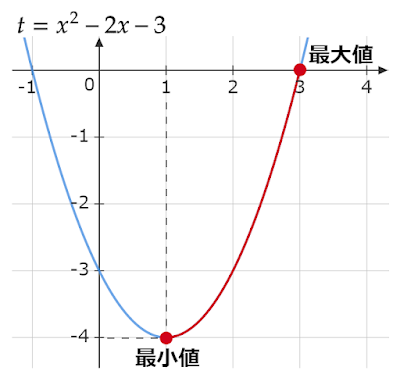
$1\leqq x\leqq3$は$x$の変域、すなわち$x$の関数である$\text{(d)}$の定義域なので最大値と最小値を求めると

上のグラフより
$x=1$のとき最小値$-4$、$x=3$のとき最大値$0$となるから$t$の変域は$-4\leqq t\leqq0$となります。

関連：2次関数の最大値・最小値を求める

ここで、$\text{(c)}$は$t$の関数であるから$t$の変域によって$y$の変域が決まります。すなわち$t$の変域は$\text{(c)}$の定義域であることがわかります。
これをもとに$\text{(c)}$の最大値と最小値を求めると

上のグラフより
$t=-\dfrac{3}{2}$のとき最小値$\dfrac{3}{4}$、$t=-4$のとき最大値$7$となります。

これは$y$の最大値と最小値なので求める答えまであと一歩です。

あとは、それぞれの$t$の値のときの$x$の値を求めればよいので$\text{(d)}$に代入して$x$について解くと

$$\begin{align*}t=-\frac{3}{2}のとき\\ -\frac{3}{2}&=(x-1)^2-4\\[0.5em](x-1)^2&=\frac{5}{2}\\[0.5em]x-1&=\pm\sqrt{\frac{5}{2}}=\pm\frac{\sqrt{10}}{2}\\[0.5em]x&=\frac{2\pm\sqrt{10}}{2}\\[0.5em]x&=\frac{2+\sqrt{10}}{2}&(\because1\leqq x\leqq3)\\[1em]t=-4のとき\\ -4&=(x-1)^2-4\\[0.5em](x-1)^2=0\\[0.5em]x-1&=0\\[0.5em]x&=1\end{align*}$$

したがって、

$$\begin{align*}x=\frac{2+\sqrt{10}}{2}のとき最小値\frac{3}{4}\\[0.5em]x=1のとき最大値7\end{align*}$$

これが求める答えです。

$y=(x^2-2x-3)^2+3(x^2-2x-3)+3$のグラフでは上のようになります。

(2)

　(1)と同様にして$x^2+4x-3=t$とおくと

$$\begin{align*}y&=t^3-t^2-t+2\tag{e}\\[1em]t&=x^2+4x-3\tag{f}\end{align*}$$

$\text{(e)}$は3次関数、$\text{(f)}$は2次関数です。$\text{(f)}$を平方完成すると

$$t=(x+2)^2-7\tag{g}$$

となります。

$0\leqq x\leqq1$における$\text{(g)}$の最大値と最小値を求めると

上のグラフより
$x=0$のとき最小値$-3$、$x=1$のとき最大値$2$となるから$t$の変域は$-3\leqq t\leqq2$となります。

$t$の変域は$\text{(e)}$の定義域なので、これをもとに$\text{(e)}$の最大値と最小値を求めます。3次関数の最大値と最小値を求めるには増減表を作ります。
$\text{(e)}$を$t$で微分すると

$$y'=3t^2-2t-1=(3t+1)(t-1)$$

$y'=0$となるような$t$は

$$\begin{align*}(3t+1)(t-1)&=0\\[0.5em]t&=-\frac{1}{3},1\end{align*}$$

であり、これらは-3\leqq t&\leqq2を満たすので、これをもとに増減表をつくると

となります。

増減表より$t=-3$のとき最小値$-31$、$t=2$のとき最大値$4$となります。

あとは、それぞれの$t$の値のときの$x$の値を求めればよいので(c)に代入して$x$について解くと

$$\begin{align*}t=-3のとき\\ -3&=x^2+4x-3\\[0.5em]x^2-4x&=0\\[0.5em]x(x+4)&=0\\[0.5em]x&=-4,0\\[0.5em]x&=0&(\because0\leqq x\leqq1)\\[1em]t=2のとき\\ 2&=x^2+4x-3\\[0.5em]x^2+4x-5&=0\\[0.5em](x+5)(x-1)&=0\\[0.5em]x&=-5,1\\[0.5em]x&=1&(\because0\leqq x\leqq1)\end{align*}$$

したがって、

$$\begin{align*}x=0のとき最小値-31\\[0.5em]x=1のとき最大値4\end{align*}$$

これが求める答えです。

$y=(x^2+4x-3)^3-(x^2+4x-3)^2-(x^2+4x-3)+2$

のグラフでは上のようになります。

関連：平方完成するには

関連：2次関数の最大値・最小値を求める