正八角形の面積を求める

「上図の正八角形の面積を求めよ。」

このような問題はどのように解けばよいのでしょうか？

(1)

この正八角形は対辺の距離のみがわかっています。

この正八角形の面積を求めるには上図のように正方形で囲みます。この正方形の1辺の長さは正八角形の対辺の距離に等しいので$10$です。

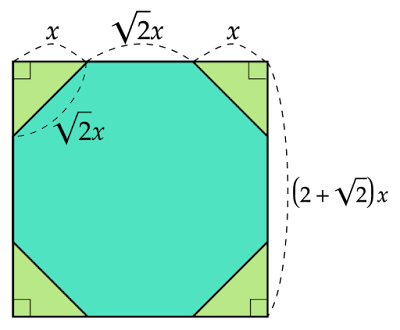
また、正八角形の1つの内角の大きさは$135°$なので、正八角形からはみ出した部分（緑）である直角三角形の直角以外の内角は$45°$となり、直角二等辺三角形であることがわかります。

関連：多角形の内角の和と正多角形の1つの内角の大きさ

ところで、直角二等辺三角形の等辺と斜辺の長さの比は$1:\sqrt{2}$です。

したがって、緑の直角二等辺三角形の等辺の長さを$x$とおけば、斜辺の長さは$\sqrt{2}x$となります。これは正八角形の1辺の長さでもあります。

正八角形を囲む正方形の1辺の長さは$10$ですが、$x$をもちいて表すと直角二等辺三角形の等辺2本と斜辺の長さの和、すなわち直角二等辺三角形の周の長さに等しいので$x+x+\sqrt{2}x=(2+\sqrt{2})x$となります。

このことから直角二等辺三角形の等辺の長さ$x$は

$$\begin{align*}(2+\sqrt{2})x&=10\\[0.5em]x&=\frac{10}{2+\sqrt{2}}\\[0.5em]&=5(2-\sqrt{2})\end{align*}$$

であるとわかります。

　正八角形の面積は、正方形の面積から4つの直角二等辺三角形の面積を引けば良いので

$$\begin{align*}正方形の面積:\\ 10^2&=100\\[1em]4つの直角二等辺三角形の面積:\\ 4\times\frac{1}{2}\times\{5(2-\sqrt{2})\}^2&=2\times5^2\times(2-\sqrt{2})^2\\[0.5em]&=2\times25(6-4\sqrt{2})\\[0.5em]&=300-200\sqrt{2}\end{align*}$$

より

$$\begin{align*}100-\left(300-200\sqrt{2}\right)&=100-300+200\sqrt{2}\\[0.5em]&=200\sqrt{2}-200\end{align*}$$

と求められます。

(2)

　この正八角形は最も遠い対角同士の距離のみがわかっています。

この正八角形の面積を求めるには、上図のように最も遠い対角同士を結ぶ対角線を引きます。このとき、すべての対角線は互いの中点で交わり、8つの合同な頂角が$45°$の二等辺三角形ができます。
二等辺三角形の等辺の長さは、最も遠い対角同士の距離の半分なので$6$です。

　この二等辺三角形に着目します。

底角の1つから対辺へ垂線を下ろすと、上図の緑の部分は鋭角が$45°$の直角三角形なので直角二等辺三角形となります。

前述の通り、直角二等辺三角形の等辺と斜辺の比は$1:\sqrt{2}$であり、この直角二等辺三角形の斜辺の長さはもとの二等辺三角形の等辺の長さの$6$であることから、直角二等辺三角形の等辺の長さ（$x$とおく）は

$$\begin{align*}x:6&=1:\sqrt{2}\\[0.5em]\sqrt{2}x&=6\\[0.5em]x&=\frac{6}{\sqrt{2}}\\[0.5em]&=\frac{6\sqrt{2}}{2}\\[0.5em]&=3\sqrt{2}\end{align*}$$

となることがわかります。

上図のように二等辺三角形の等辺の1つを底辺としたとき、高さは直角二等辺三角形の等辺となるので、二等辺三角形の面積は

$$\frac{1}{2}\times6\times3\sqrt{2}=9\sqrt{2}$$

となります。

　正八角形の面積は二等辺三角形の8倍なので

$$9\sqrt{2}\times8=72\sqrt{2}$$

と求められます。

関連：円に内接・外接する正多角形の面積を求める公式を作ってみよう