多角形の内角の和の求め方 正多角形の1つの内角の大きさの求め方

　多角形の内角の和はどのように求めるのでしょうか？
また、正多角形の1つの内角の大きさはどのように求めるのでしょうか？

多角形の内角の和

まず、三角形の内角の和は以下のようにして$180°$であることがわかります。

$△ABC$の頂点$C$を通る辺$AB$に平行な直線を引き、この平行線上に直線$BC$に関して頂点$A$と同じ側に点$D$をとります。また、辺$BC$の頂点$C$側の延長上に点$E$をとります。

すると、平行線の錯角より$∠A=∠ACD$、平行線の同位角より$∠B=∠DCE$となります。
1本の直線のつくる角の大きさは$180°$なので、$∠ACB+∠ACD+∠DCE=180°$です。
これは$△ABC$の内角の和$∠A+∠B+∠ACB$に等しいので、三角形の内角の和は$180°$であることがわかります。

　三角形以外の多角形は、この三角形の内角の和が$180°$であることを利用して求めます。

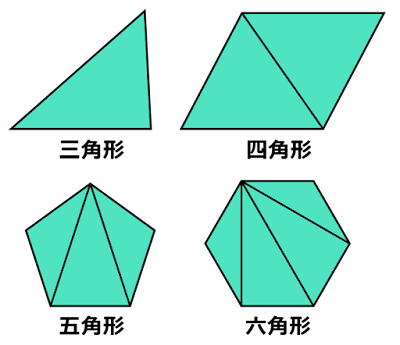
三角形以外の多角形は対角線を引くことができます。この対角線を互いに交わらないように引き、いくつかの三角形をつくります。

対角線の引き方で簡単なのは、1つの頂点から他の頂点へ対角線を引くことです。
このとき、始点となる頂点自身とその両隣の頂点へは対角線を引くことはできないので、1つの頂点から引くことができる対角線の本数は頂点の数より$3$だけ少なくなります。

四角形は$1$本、五角形は$2$本、…、頂点の数が$n$個の$n$角形は$n-3$本となります。

この対角線によって多角形は対角線の本数より1つ多く分割されるので、$n$角形は$(n-3)+1=n-2$個の三角形に分割されます。
ちなみに、これらは三角形（$n=3$）の場合でも成り立ちます。対角線は$3-3=0$本、三角形の個数は$3-2=1$個です。

分割された三角形の内角はすべて元の多角形の内角の一部なので、すべての三角形の内角の和と多角形の内角の和は等しくなります。

1つの三角形の内角の和は$180°$なので、$n$角形の内角の和は

$$\large (n-2)×180°$$

で求めることができます。

正多角形の1つの内角の大きさ

　正多角形のすべての内角の大きさは等しいので、内角の和を頂点の個数で割ったものが1つの内角の大きさとなります。

正$n$角形の内角の和は$(n-2)×180°$なので、1つの内角の大きさは

$$\large \frac{(n-2)}{n}×180°$$

で求めることができます。