「次の不等式を解け。
(1)$\large (x+2)^3<8$
(2)$\large (x+1)^2(x-2)\leqq0$
(3)$\large x(x+2)(x-5)>0$」
積の正負から解く方法とグラフから解く方法の2通りで解いてみます。
(1)$(x+2)^3<8$
1. 積の正負から解く
移項した$(x+2)^3-8<0$を因数分解します。
左辺は
\begin{align*}(x+2)^3-8&=(x+2)^3-2^3\\[0.5em]a=x+2,b=2とおくと\\
a^3-b^3=(a-b)(a^2+ab+b^2)より\\
(x+2)^3-2^3&={(x+2)-2}{(x+2)^2+2(x+2)+2^2}\\[0.5em]&=x(x^2+6x+12)\end{align*}
と因数分解できるので$x(x^2+6x+12)<0$となります。
ここで、積の正負について考えると以下のようになります。
\begin{align*}(正)×(正)&=(正)&(正)×(負)&=(負)\\[0.5em](負)×(正)&=(負)&(負)×(負)&=(正)\end{align*}
これを踏まえると、不等式が成り立つためには「$x<0$かつ$x^2+6x+12>0$」または「$x>0$かつ$x^2+6x+12<0$」のいずれかが成り立つことが条件となります。
1-1. $x<0$かつ$x^2+6x+12>0$
$x^2+6x+12$を平方完成すると
\begin{align*}x^2+6x+12&=(x^2+6x+9)-9+12\\[0.5em]&=(x+3)^2+3\end{align*}
となるから最小値が$3$、すなわち常に$x^2+6x+12>0$であるので、すべての実数$x$において成り立ちます。
$x<0$と$x^2+6x+12>0$は「かつ」で結ばれているので、2つの$x$の範囲の共通部分が不等式の解となります。
したがって、「$x<0$かつ$x^2+6x+12>0$」を満たす$x$の範囲は$x<0$となります。
1-2. $x>0$かつ$x^2+6x+12<0$
$x^2+6x+12<0$を解くと解なしとなります。これは常に$x^2+6x+12>0$が成り立つことからもわかります。
$x^2+6x+12<0$が成り立たないので「$x>0$かつ$x^2+6x+12<0$」が成り立つような$x$は存在しないことになります。
1-1.、1-2.より$(x+2)^3<8$の解は$x<0$であるとわかります。
2. グラフから解く
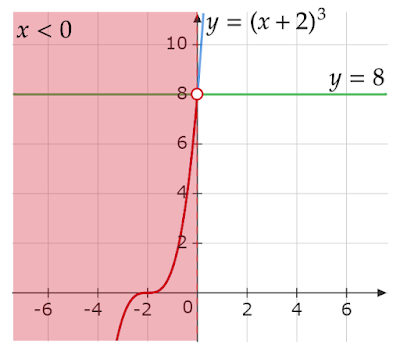
$y=(x+2)^3$と$y=8$のグラフを考えます。
$y=(x+2)^3$は$y=x^3$のグラフをx軸方向に$-2$だけ平行移動したもの、$y=8$はすべてのy座標が$8$の点を通る直線なのでグラフは以下のようになります。
$y=(x+2)^3$のグラフのうち、$y<8$となる部分が存在する$x$の範囲が不等式の解となります。グラフから$x<0$と読み取れるので、これが解となります。
(2)$(x+1)^2(x-2)\leqq0$
1. 積の正負から解く
不等式が成り立つためには「$(x+1)^2\leqq0$かつ$x-2\geqq0$」または「$(x+1)^2\geqq0$かつ$x-2\leqq0$」のいずれかが成り立つことが条件となります。
1-1. $(x+1)^2\leqq0$かつ$x-2\geqq0$
$(x+1)^2\leqq0$において成り立つのは$(x+1)^2=0$のみなので、$x+1=0$すなわち$x=-1$が解となります。
$x-2\geqq0$を解くと$x\geqq2$です。
これらの共通部分はないので、「$(x+1)^2\leqq0$かつ$x-2\geqq0$」を満たす$x$は存在しません。
1-2. $(x+1)^2\geqq0$かつ$x-2\leqq0$
$(x+1)^2\geqq0$、これは2乗の性質そのままなので、すべての実数$x$において成り立ちます。
$x-2\leqq0$を解くと$x\leqq2$です。
これらの共通部分は$x\leqq2$なので、これが「$(x+1)^2\geqq0$かつ$x-2\leqq0$」を満たす$x$の範囲となります。
1-1.、1-2より$(x+1)^2(x-2)\leqq0$の解は$x\leqq2$であるとわかります。
2. グラフから解く
$y=(x+1)^2(x-2)$のグラフは以下のようになります。
このグラフの$y\leqq0$の部分が存在する$x$の範囲は$x\leqq2$で、これが$(x+1)^2(x-2)\leqq0$の解となります。
(3)$x(x+2)(x-5)>0$
1. 積の正負から解く
(1)、(2)とは異なり因数が3つありますが、$x(x+2)$と$x-5$のように2つに分けて解くことができます。
不等式が成り立つためには「$x(x+2)<0$かつ$x-5<0$」または「$x(x+2)>0$かつ$x-5>0$」のいずれかが成り立つことが条件となります。
1-1. $x(x+2)<0$かつ$x-5<0$
$x(x+2)<0$を解くと$-2<x<0$となります。
$x-5<0$を解くと$x<5$です。
これらの共通部分は$-2<x<0$なので、これが「$x(x+2)<0$かつ$x-5<0$」を満たす$x$の範囲となります。
1-2. $x(x+2)>0$かつ$x-5>0$
$x(x+2)>0$を解くと$x<-2,0<x$となります。
$x-5>0$を解くと$x>5$です。
これらの共通部分は$x>5$なので、これが「$x(x+2)>0$かつ$x-5>0$」を満たす$x$の範囲となります。
1-1.、1-2.より$x(x+2)(x-5)>0$の解は$-2<x<0$または$x>5$であるとわかります。($-2x<0,5<x$のように並列して書くこともできます。)
2. グラフから解く
$y=x(x+2)(x-5)$のグラフは以下のようになります。
このグラフの$y>0$の部分が存在する$x$の範囲は$-2x<0,5<x$で、これが$x(x+2)(x-5)>0$の解となります。
$a>0,b=0$のとき、$y=a(x-\alpha)^2(x-\beta)$のx軸との共有点のうち、$x=\alpha$である共有点はグラフの極値を持つ点(凹部または凸部の先端部)に存在します。
凹部か凸部のどちらになるのかはもう1つの共有点のx座標$x=\beta$との大小関係で決まります。$\alpha<\beta$のときは凹部、$\alpha>\beta$のときは凸部のほうとなります。
Share:
https://p-suugaku.blogspot.com/2023/03/3jifutoushiki.html3次不等式を解く
.png)
.png)
.png)



