「次の2次不等式を解け。
(1)$\large x^2-3x-18<0$
(2)$\large x^2+6x+8\geqq0$
(3)$\large -x^2+2x-3<0$
(4)$\large x^2-4x+5\leqq0$」
2次不等式は因数に着目して解を求める方法とグラフから解を求める方法があります。
この2通りの方法で2次不等式を解いてみます。
(1)$x^2-3x-18<0$
1. 因数に着目して解を求める方法
左辺を因数分解すると
\[(x+3)(x-6)<0\]
となります。
左辺は負であるから、掛けて負となる条件を考えると
\[(正)\times(負)=(負)\quad(負)\times(正)=(負)\]
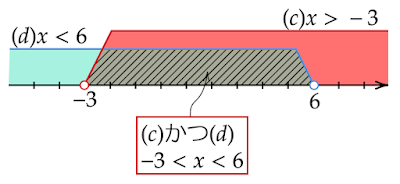
より「$x+3>0$かつ$x-6<0$ …(a)」、「$x+3<0$かつ$x-6>0$
…(b)」の2通りが考えられます。ここで、$3>-6$より$x+3>x-6$なので、(b)は不適。
したがって、「$x+3>0$かつ$x-6<0$ …(a)」を満たす$x$を求めます。
\begin{align*}x+3&>0\\ \\ x&>-3&\cdots(c)\\ \\ \\
x-6&<0\\ \\ x<6&\cdots(d)\end{align*}
2. グラフを利用して解を求める方法
グラフを利用するときは、2次不等式を「$y=x^2-3x-18$かつ$y<0$」というように分解して考えます。
$y=0$は$y$の範囲に含まれないので求める$x$の範囲にも$x=-3,6$は含まれない点には気をつけてください。
(2)$x^2+6x+8\geqq0$
1.
左辺を因数分解すると
\[(x+4)(x+2)\geqq0\]
となります。
これは「$(x+4)(x+2)>0$または$(x+4)(x+2)=0$」と分けて考えれば、おのおのから導き出される条件より不等式が満たす$x$の範囲を求めることができます。
しかし、2次不等式を解くで紹介している通り、「$x+4\leqq0$かつ$x+2\leqq0$ …(c)」、「$x+4\geqq0$かつ$x+2\geqq0$
…(d)」の2通りに分けて考えることができます。
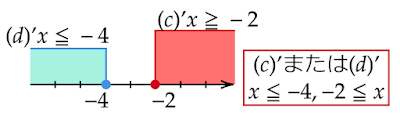
(c)の場合:
\begin{align*}x+4&\leqq0\\ \\ x&\leqq-4&\cdots(e)\\ \\ \\
x+2&\leqq0\\ \\ x&\leqq-2&\cdots(f)\end{align*}
(e)かつ(f)なので、$x\leqq-4$ …(c)'となります。
(d)の場合:
\begin{align*}x+4&\geqq0\\ \\ x&\geqq-4&\cdots(g)\\ \\ \\
x+2&\geqq0\\ \\ x&\geqq-2&\cdots(h)\end{align*}
(g)かつ(h)なので、$x\geqq-2$ …(d)'となります。2.
不等式を「$y=x^2+6x+8$かつ$y\geqq0$」というように分解します。
(3)$-x^2+2x-3<0$
1.
左辺は実数の範囲で因数分解できません。
なので、左辺を平方完成してみます。
\begin{align*}-(x^2-2x)-3&=-\{(x^2-2x+1)-1\}-3\\ \\
&=-(x^2-2x+1)-2\\ \\ &=-(x-1)^2-2\end{align*}
ここで、2乗した数は$0$以上となるので$-(x-1)^2\leqq0$となります。そして、$-2$は負の数であるから常に$-(x-1)^2-2<0$です。
$x$の値に関係なく不等式は常に成り立つので、解はすべての実数となります。
2.
x軸とは共有点を持たないので、$y$は常に負となります。
(4)$x^2-4x+5\leqq0$
1.
これも左辺は実数の範囲で因数分解できません。
左辺を平方完成すると
\begin{align*}(x^2-4x)+5&=\{(x^2-4x+4)-4\}+5\\ \\ &=(x^2-4x+4)+1\\
\\ &=(x-2)^2+1\end{align*}
$(x-2)^2\geqq0$なので、常に$(x-2)^2+1>0$です。
左辺が$0$以下になることはないので不等式が成り立つことはありません。したがって、解はありません。
2.
x軸とは共有点を持たないので、$y$は常に正となります。
問題の不等式は$y$が$0$以下になっている部分を表していますが、そのような部分はないので不等式を満たす$x$の範囲はありません。
Share:
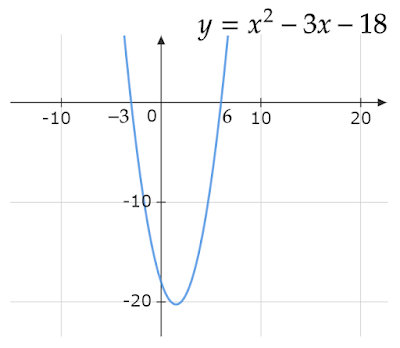
.png)

.png)
.png)
.png)
.png)



