対角線の長さとなす角から平行四辺形の面積を求める

「平行四辺形$\text{ABCD}$の対角線$\text{AC}$の長さが$4$、$\text{BD}$の長さが$6$、対角線同士のなす角が$60°$のとき、平行四辺形の面積を求めよ。」

このような問題はどのように解けばよいのでしょうか？

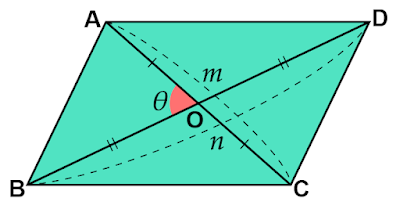
　まずは平行四辺形$\text{ABCD}$の対角線$\text{AC}$の長さが$m$、$\text{BD}$の長さが$n$、対角線同士のなす角が$\theta$の場合を考えてみます。
対角線同士の交点を$\text{O}$とすると、平行四辺形の性質より対角線は互いの中点で交わります。

関連：ひし形の対角線が互いの垂直二等分線であることの証明

したがって、

$$\begin{align*}\text{AO}=\text{CO}=\frac{m}{2}\\[1em]\text{BO}=\text{DO}=\frac{n}{2}\end{align*}$$

です。

ここで、$△\text{OAB}$の面積は

$$\begin{align*}△\text{OAB}&=\frac{1}{2}\text{AO}\cdot \text{BO}\sin\theta\\[0.5em]&=\frac{1}{2}\cdot\frac{m}{2}\cdot\frac{n}{2}\sin\theta\\[0.5em]&=\frac{mn}{8}\sin\theta\end{align*}$$

で求められます。

関連：なぜsinを使って三角形の面積を求めることができるのか？

$△\text{OAD}$の面積は$∠\text{AOD}=180°-θ$、$\sin(180°-\theta)=\sin\theta$より

$$\begin{align*}△\text{OAD}&=\frac{1}{2}\text{AO}\cdot \text{DO}\sin(180°-\theta)\\[0.5em]&=\frac{mn}{8}\sin\theta\end{align*}$$

で求められます。

関連：$-θ, 90°±θ, 180°±θ, 270°±θ$の三角関数

$△\text{OAB}$と$△\text{OCD}$、$△\text{OBC}$と$△\text{ODA}$は合同で、いずれの三角形の面積も$\dfrac{mn}{8}\sin\theta$であるから、平行四辺形$\text{ABCD}$の面積はいずれかの三角形の面積の4倍となるので、

$$\begin{align*}□\text{ABCD}&=4\cdot\frac{mn}{8}\sin\theta\\[0.5em]&=\frac{mn}{2}\sin\theta\end{align*}$$

であるとわかります。

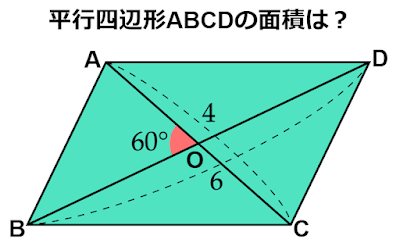
　問題の場合$m=4, n=6, \theta=60°$なので、上の式に代入すると

$$\begin{align*}□\text{ABCD}&=\frac{4\cdot6}{2}\sin60°\\[0.5em]&=12\cdot\frac{\sqrt{3}}{2}\\[0.5em]&=6\sqrt{3}\end{align*}$$

となります。

関連：三角比で平行四辺形の面積を求める