三角形の面積を求める式いろいろ

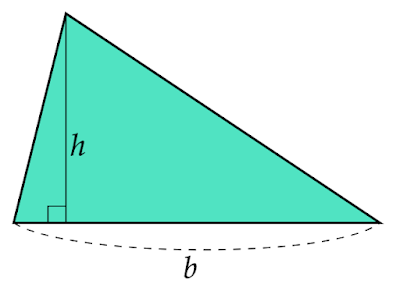
底辺の長さと高さを利用

　三角形の底辺の長さ$b$と高さ$h$を使って三角形の面積$S$を求めると

$$S=\frac{1}{2}bh$$

となります。

高さとは底辺の端点でない頂点から底辺までの最短距離です。

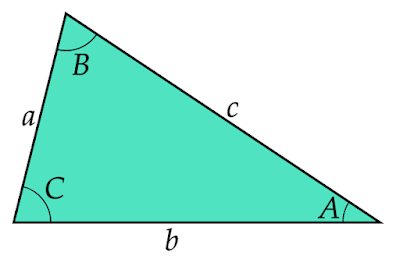
2辺とその間の角を利用

　三角形の3辺$a, b, c$と対角$\text{A, B, C}$のうち2辺とその間の角を使って三角形の面積$S$を求めると

$$S=\frac{1}{2}ab\sin \text{C}=\frac{1}{2}bc\sin \text{A}=\frac{1}{2}ca\sin \text{B}$$

となります。

関連：なぜsinを使って三角形の面積を求めることができるのか？

3辺の長さを利用

　三角形の3辺$a, b, c$を使って三角形の面積$S$を求めると

$$\begin{align*}S=\sqrt{s(s-a)(s-b)(s-c)}\\ ただし、&s=\frac{a+b+c}{2}\end{align*}$$

となります。これはヘロンの公式と呼ばれます。

関連：ヘロンの公式　三角形の3辺から面積を求める公式

座標平面上の三角形

　座標平面上の3点$\text{A}(a_1, a_2), \text{B}(b_1, b_2), \text{C}(c_1, c_2)$よりできる$△\text{ABC}$において
ベクトルと2辺とその間の角を利用した三角形の面積の求め方から

$$\begin{align*}S&=\frac{1}{2}|\vec{\text{AB}}||\vec{\text{AC}}|\sin∠\text{BAC}\\[0.5em]&=\frac{1}{2}|(b_1-a_1)(c_2-a_2)-(b_2-a_2)(c_1-a_1)|\\[1.5em]S&=\frac{1}{2}|\vec{\text{BC}}||\vec{\text{BA}}|\sin∠\text{ABC}\\[0.5em]&=\frac{1}{2}|(c_1-b_1)(a_2-b_2)-(c_2-b_2)(a_1-b_1)|\\[1.5em]S&=\frac{1}{2}|\vec{\text{CA}}||\vec{\text{CB}}|\sin∠\text{ACB}\\[0.5em]&=\frac{1}{2}|(a_1-c_1)(b_2-c_2)-(a_2-c_2)(b_1-c_1)|\end{align*}$$

となります。

関連：原点と他の2点から作られる三角形の面積を求める

座標空間内の三角形

　座標空間内の3点$\text{A}(a_1, a_2, a_3), \text{B}(b_1, b_2, b_3), \text{C}(c_1, c_2, c_3)$よりできる$△\text{ABC}$において
ベクトルの外積を利用して面積$S$は

$$\begin{align*}S&=\frac{1}{2}|\vec{\text{AB}}\times\vec{\text{AC}}|\\[0.5em]&=\frac{1}{2}\sqrt{\begin{aligned}&\left\{(b_2-a_2)(c_3-a_3)-(b_3-a_3)(c_2-a_2)\right\}^2\\ &\quad+\left\{(b_3-a_3)(c_1-a_1)-(b_1-a_1)(c_3-a_3)\right\}^2\\ &\quad+\left\{(b_1-a_1)(c_3-a_3)-(b_3-a_3)(c_1-a_1)\right\}^2\end{aligned}}\\[1.5em]S&=\frac{1}{2}|\vec{\text{BC}}\times\vec{\text{BA}}|\\[0.5em]&=\frac{1}{2}\sqrt{\begin{aligned}&\left\{(c_2-b_2)(a_3-b_3)-(c_3-b_3)(a_2-c_2)\right\}^2\\ &\quad+\left\{(c_3-b_3)(a_1-b_1)-(c_1-b_1)(a_3-c_3)\right\}^2\\ &\quad+\left\{(c_1-b_1)(a_3-b_3)-(c_3-b_3)(a_1-b_1)\right\}^2\end{aligned}}\\[1.5em]S&=\frac{1}{2}|\vec{\text{CA}}\times\vec{\text{CB}}|\\[0.5em]&=\frac{1}{2}\sqrt{\begin{aligned}&\left\{(a_2-c_2)(b_3-c_3)-(a_3-c_3)(b_2-c_2)\right\}^2\\ &\quad+\left\{(a_3-c_3)(b_1-c_1)-(a_1-c_1)(b_3-c_3)\right\}^2\\ &\quad+\left\{(a_1-c_1)(b_3-c_3)-(a_3-c_3)(b_1-c_1)\right\}^2\end{aligned}}\end{align*}$$

となります。※根号の中が非常に長いため改行してあります。