ルーローの三角形の周の長さと面積を求める

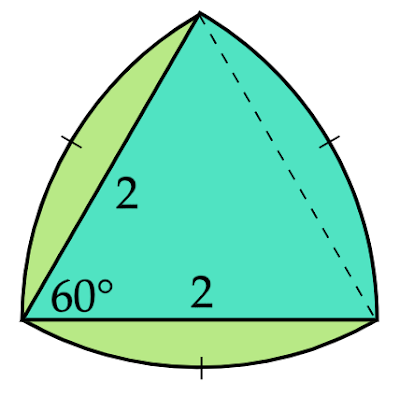
「上の図形は正三角形の各頂点を中心とし、1辺の長さを半径とする円弧で他の2つの頂点間を結んだ図形で、ルーローの三角形と呼ばれる。
この図形を作図するときにもとになった正三角形の1辺の長さが$2$であったとき、この図形の周の長さと面積を求めよ。」

このような問題はどのように解けばよいのでしょうか？

　ルーローの三角形は3つの合同な中心角$60°$のおうぎ形を$120°$ずつずらして重ねたような形をしています。
したがって、ルーローの三角形の周の長さは中心角$60°$のおうぎ形の弧の長さの3倍に等しいことがわかります。

半径$r$、中心角$\theta$のおうぎ形の弧の長さ$l$は

\[l=2\pi r\times\frac{\theta}{360°}\]

であるから、半径が$2$、中心角が$60°$のおうぎ形の弧の長さは

\begin{align*}l&=2\times2\times\pi\times\frac{60°}{360°}\\[0.5em]&=4\pi\times\frac{1}{6}\\[0.5em]&=\frac{2}{3}\pi\end{align*}

となります。

したがって、ルーローの三角形の周の長さはこの3倍なので$\large 2\pi$であるとわかります。

　ルーローの三角形は、中心角$60°$のおうぎ形の面積と2つの弓形でできているので、それぞれの面積を求めます。

半径$r$、中心角$\theta$のおうぎ形の面積$S$は

\[S=\pi r^2\times\frac{\theta}{360°}\]

であるから、半径が$2$、中心角が$60°$のおうぎ形の面積は

\begin{align*}S&=2^2\pi\times\frac{60°}{360°}\\[0.5em]&=4\pi\times\frac{1}{6}\\[0.5em]&=\frac{2}{3}\pi\end{align*}

となります。

　次に弓形はおうぎ形から正三角形を引いた形をしています。
面積を求めるにはまずは正三角形の面積を求める必要があります。

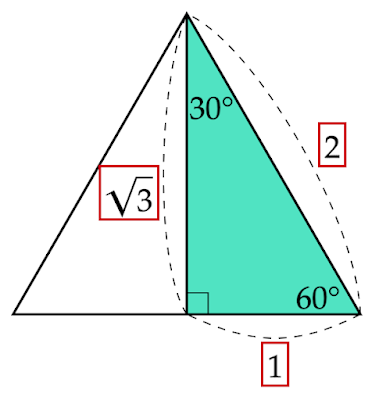
正三角形を頂点から対辺に垂線を下ろすと$30°-60°-90°$の直角三角形ができます。この直角三角形の3辺の比は$1:2:\sqrt{3}$で正三角形の高さにあたる辺の長さは1辺の長さが$2$であるとき$\sqrt{3}$です。
このことから、正三角形の面積は

\[\frac{1}{2}\times2\times\sqrt{3}=\sqrt{3}\]

となります。

上記よりおうぎ形の面積は$\dfrac{2}{3}\pi$であるから、弓形の面積は

\[\frac{2}{3}\pi-\sqrt{3}\]

と求められます。

　以上よりルーローの三角形の面積は

\[\frac{2}{3}\pi+2\times\left(\frac{2}{3}\pi-\sqrt{3}\right)=2\pi+2\sqrt{3}\]

であることがわかります。