円に内接する四角形の面積を求める方法　ブラーマグプタの公式 ~ 数学について考えてみる

　円に内接する四角形の4辺の長さがわかっているとき、この四角形の面積

$\text{S}$ は

$\begin{align*}\text{S}=\sqrt{(s-a)(s-b)(s-c)(s-d)}\\ ただし、&s=\frac{a+b+c+d}{2}\end{align*}$

で求めることができます。この式をブーラマグプタの公式と呼びます。

なぜこの式で面積を求めることができるのでしょうか？

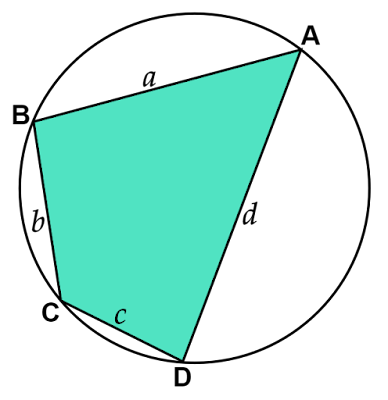
　円に内接する四角形

$\text{ABCD}$ の各辺の長さを

$\text{AB}=a,\text{BC}=b,\text{CD}=c,\text{DA}=d$ とします。

$∠\text{ABC}=\theta$ とすると、円に内接する四角形の対角の和は

$180°$ なので、

$∠\text{CDA}=180°-\theta$ となります。

対角線

$\text{AC}$ を引き、その長さを

$e$ とおくと、余弦定理より

$△\text{ABC}$ において

$\begin{equation}e^2=a^2+b^2-2ab\cos\theta\end{equation}$

$△\text{CDA}$ において

$\begin{equation}e^2=c^2+d^2-2cd\cos(180°-\theta)\end{equation}$

となります。

ここで、三角関数の性質より

$\cos(180°-\theta)=-\cos\theta$ なので、

$(2)$ は

$\begin{align*}e^2&=c^2+d^2-2cd(-\cos\theta)\\[0.5em]&=c^2+d^2+2cd\cos\theta\tag3\end{align*}$

となります。

$(1),(3)$ を連立して

$\cos\theta$ について解くと

$\begin{align*}a^2+b^2-2ab\cos\theta&=c^2+d^2+2cd\cos\theta\\[0.5em]2(ab+cd)\cos\theta&=a^2+b^2-c^2-d^2\\[0.5em]\cos\theta&=\frac{a^2+b^2-c^2-d^2}{2(ab+cd)}\tag4\end{align*}$

$□\text{ABCD}$ の面積を

$\text{S}$ とすると

$\begin{align*}\text{S}&=△\text{ABC}+△\text{CDA}\\[0.5em]&=\frac{1}{2}ab\sin\theta+\frac{1}{2}cd\sin(180°-\theta)\end{align*}$

となります。

ここで、三角関数の性質より

$\sin(180°-\theta)=\sin\theta$ なので、

$\begin{align*}\text{S}&=\frac{1}{2}ab\sin\theta+\frac{1}{2}cd\sin\theta\\[0.5em]&=\frac{1}{2}(ab+cd)\sin\theta\end{align*}$

また、三角関数の相互関係

$\sin^2\theta+\cos^2\theta=1$ より、

$0°<\theta<180°$ のとき

$\sin\theta=\sqrt{1-\cos^2\theta}$ なので、

$\text{S}=\frac{1}{2}(ab+cd)\sqrt{1-\cos^2\theta}$

となります。

これに

$(4)$ を代入して

$\begin{align*}\text{S}&=\frac{1}{2}(ab+cd)\sqrt{1-\left(\frac{a^2+b^2-c^2-d^2}{2(ab+cd)}\right)^2}\\[0.5em]&=\frac{1}{2}(ab+cd)\sqrt{\frac{4(ab+cd)^2-(a^2+b^2-c^2-d^2)^2}{4(ab+cd)^2}}\\[0.5em]&=\frac{1}{2}(ab+cd)\cdot\frac{1}{2(ab+cd)}\sqrt{4(ab+cd)^2-(a^2+b^2-c^2-d^2)^2}\\[0.5em]&=\frac{1}{4}\sqrt{4(ab+cd)^2-(a^2+b^2-c^2-d^2)^2}\\[0.5em]&=\frac{1}{4}\sqrt{\begin{aligned}&\left\{2(ab+cd)-(a^2+b^2-c^2-d^2)\right\}\\ &\quad\cdot\left\{2(ab+cd)+(a^2+b^2-c^2-d^2)\right\}\end{aligned}}\\[0.5em]&=\frac{1}{4}\sqrt{\begin{aligned}&\left\{(c^2+2cd+d^2)-(a^2-2ab+b^2)\right\}\\ &\quad\cdot\left\{(a^2+2ab+b^2)-(c^2-2cd+d^2)\right\}\end{aligned}}\\[0.5em]&=\frac{1}{4}\sqrt{\begin{aligned}&\left\{(c+d)^2-(a-b)^2\right\}\\ &\quad\cdot\left\{(a+b)^2-(c-d)^2\right\}\end{aligned}}\\[0.5em]&=\frac{1}{4}\sqrt{\begin{aligned}&\left\{(c+d)-(a-b)\right\}\left\{(c+d)+(a-b)\right\}\\ &\quad\cdot\left\{(a+b)-(c-d)\right\}\left\{(a+b)+(c-d)\right\}\end{aligned}}\\[0.5em]&=\frac{1}{4}\sqrt{\begin{aligned}&(-a+b+c+d)(a-b+c+d)\\ &\quad\cdot(a+b-c+d)(a+b+c-d)\end{aligned}}\\[0.5em]&=\frac{1}{4}\sqrt{\begin{aligned}&\left\{(a+b+c+d)-2a\right\}\left\{(a+b+c+d)-2b\right\}\\ &\quad\cdot\left\{(a+b+c+d)-2c\right\}\left\{(a+b+c+d)-2d\right\}\end{aligned}}\end{align*}$

※5行目から根号内で改行しています。

ここで、

$s=\dfrac{a+b+c+d}{2}$ とおくと

$\begin{align*}\text{S}&=\frac{1}{4}\sqrt{(2s-2a)(2s-2b)(2s-2c)(2s-2d)}\\[0.5em]&=\frac{1}{4}\sqrt{2(s-a)\cdot2(s-b)\cdot2(s-c)\cdot2(s-d)}\\[0.5em]&=\frac{1}{4}\sqrt{16(s-a)(s-b)(s-c)(s-d)}\\[0.5em]&=\frac{1}{4}\cdot4\sqrt{(s-a)(s-b)(s-c)(s-d)}\\[0.5em]&=\sqrt{(s-a)(s-b)(s-c)(s-d)}\end{align*}$

となります。

式の形や導出過程がヘロンの公式と似ています。

　円に内接する四角形が内接円を持つとき、四角形の4辺はすべて内接円の接線で、四角形の頂点は2本の接線の交点となります。

辺

$\text{AB, BC, CD, DA}$ と内接円の接点をそれぞれ

$\text{E, F, G, H}$ とすると、2本の接線の交点から接点までの距離は等しいので、各線分の長さを

$\begin{cases}\text{AE}=\text{HA}=w\\[0.5em]\text{EB}=\text{BF}=x\\[0.5em]\text{FC}=\text{CG}=y\\[0.5em]\text{GD}=\text{DH}=z\end{cases}$

とすると

$\begin{cases}a=w+x\\[0.5em]b=x+y\\[0.5em]c=y+z\\[0.5em]d=z+w\end{cases}$

また、

$a+b+c+d=2w+2x+2y+2z$ より

$s=w+x+y+z$ なので、ブラーマグプタの公式に代入すると

$\begin{align*}\text{S}&=\sqrt{\begin{aligned}&\left\{(w+x+y+z)-(w+x)\right\}\left\{(w+x+y+z)-(x+y)\right\}\\ &\quad\cdot\left\{(w+x+y+z)-(y+z)\right\}\left\{(w+x+y+z)-(z+w)\right\}\end{aligned}}\\[0.5em]&=\sqrt{(y+z)(z+w)(w+x)(x+y)}\\[0.5em]&=\sqrt{cdab}=\sqrt{abcd}\end{align*}$

となります。