なぜsinを使って三角形の面積が求められるのか？

図1　三角形\text{ABC}

　三角比を利用して図1のような三角形$\text{ABC}$の面積は

$$\begin{equation}△\text{ABC}=\frac{1}{2}\text{AB}\cdot\text{AC}\sinθ\end{equation}$$

で求めることができます。

なぜこの式で三角形の面積を求めることができるのでしょうか？

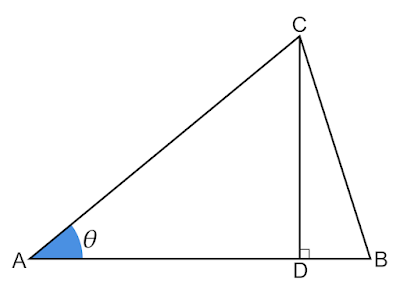
図2　\text{AB}に対して\text{C}から垂線を引く

　図2のように頂点\text{C}から辺$\text{AB}$に垂線を下ろし交点を$\text{D}$とします。
$△\text{ADC}$は直角三角形で$\text{CD}$の長さが$△\text{ABC}$の高さとなります。

三角比を利用して$\text{CD}$の長さを求めると

$$\begin{align*}\sinθ&=\frac{\text{CD}}{\text{AC}}\\[0.5em]\text{CD}&=\text{AC}\sinθ\end{align*}$$

したがって、$△\text{ABC}$の面積は

$$\begin{align*}△\text{ABC}&=\frac{1}{2}\text{AB}\cdot\text{CD}\\[0.5em]&=\frac{1}{2}\text{AB}\cdot\text{AC}\sinθ\end{align*}$$

となり、$(1)$と同じ式を導くことができました。

　先程は$∠\text{A}$が鋭角の場合なので、鈍角である場合についても考えます。

図3　∠\text{A}が鈍角である場合

半直線$\text{BA}$に対して頂点$\text{C}$から垂線を下ろし、その交点を$\text{D}$とします。
$△\text{DAC}$は直角三角形で、$\text{CD}$は$△\text{ABC}$の高さに相当します。また、$∠\text{DAC}$は$∠\text{A}$の外角であるため$180°-θ$です。

$$\begin{align*}\sin(180°-θ)&=\frac{\text{CD}}{\text{AC}}\\[0.5em]\text{CD}&=\text{AC}\sin(180°-θ)\end{align*}$$

$\sin(180°-θ)=\sinθ$なので

$$\text{CD}=\text{AC}\sinθ$$

したがって、$△\text{ABC}$の面積は

$$\begin{align*}△\text{ABC}&=\frac{1}{2}\text{AB}\cdot\text{CD}\\[0.5em]&=\frac{1}{2}\text{AB}\cdot\text{AC}\sinθ\end{align*}$$

となり、こちらも$(1)$と同じ式となることがわかりました。

関連：三角比で平行四辺形の面積を求める