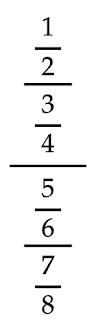まずは以下のように割り算に変換して割られる数と割る数に分けて考えます。
\[\frac{\ \cfrac{1}{2}\ }{\cfrac{3}{4}}÷\frac{\ \cfrac{5}{6}\
}{\cfrac{7}{8}}\]
割られる数
二重の入れ子になっている分数を先ほどと同じように割り算で表すと、
\[\frac{\ \cfrac{1}{2}\ }{\cfrac{3}{4}}=\frac{1}{2}÷\frac{3}{4}\]
あとは掛け算に変換して、簡単にすると
\[\frac{1}{2}×\frac{4}{3}=\frac{2}{3}\]
となります。
あるいは最も内側の分数の分母の公倍数をそれぞれにかけて、(例の場合は2と4の公倍数の4)
\begin{align*}\frac{\ \cfrac{1}{2}\ }{\cfrac{3}{4}}&=\frac{\
\cfrac{1}{2}×4\ }{\cfrac{3}{4}×4}\\[0.5em]&=\frac{2}{3}\end{align*}
のように計算します。
割る数
割る数の方も、割られる数と同様に計算して、
\begin{align*}\frac{\ \cfrac{5}{6}\ }{\cfrac{7}{8}}&=\frac{\
\cfrac{5}{6}×24\ }{\cfrac{7}{8}×24}\\[0.5em]&=\frac{5×4}{7×3}=\cfrac{20}{21}\end{align*}
再び割られる数と割る数を分数に戻すと
\[\frac{\ \cfrac{2}{3}\ }{\cfrac{20}{21}}\]
となります。
これに先程の計算をすれば、
\begin{align*}\frac{\ \cfrac{2}{3}\ }{\cfrac{20}{21}}&=\frac{\
\cfrac{2}{3}×21\ }{\cfrac{20}{21}×21}\\[0.5em]&=\frac{2×
7}{20}=\frac{7}{10}\end{align*}
このように求めることができます。
Share: