時計の針と角度

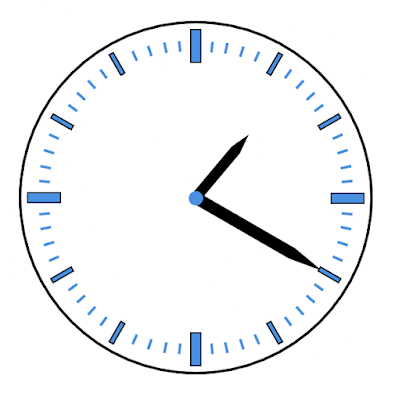
　時計の目盛りは1から12までの数字が振ってある大きな目盛りは12個、大きな目盛りと大きな目盛りの間には小さな目盛りが4個あります。それぞれ1目盛り何度あるでしょうか？

1周360°なので、

$$360^{\circ}÷12=\underline{30^{\circ}}$$

小さな目盛りは、大きな目盛りを5等分しているので、

$$30^{\circ}÷5=\underline{6^{\circ}}$$

　時針は12時間で1周、分針は1時間で1周するので、それぞれが1分あたりに進む角度は、

時針：$\frac{360^{\circ}}{12× 60}=0.5^{\circ}$なので0.5°/分

分針：$\frac{360^{\circ}}{1× 60}=6^{\circ}$なので6°/分

となります。

例題

「アナログ時計が1時20分を示している。このとき、時針と分針のなす角のうち小さい方の角度は何度になるか？」

という問題について考えてみます。

12の目盛りを基準とすると分針は4の位置にあるので、

$$30^{\circ}× 4=120^{\circ}$$

時針は1の目盛りから20分進んだ位置にあるので、

$$\begin{align*}30^{\circ}+0.5^{\circ}× 20&=30^{\circ}+10^{\circ}\\ &=40^{\circ}\end{align*}$$

となります。

したがって、求める角度は分針の角度と時針の角度の差なので、80°となります。