1つの辺の長さがわかれば面積が求められる特殊な三角形

　通常、三角形の面積は

\[(底辺)\times(高さ)\div2\]

で表されるように、底辺と高さという2つの長さがわからないと求められません。

しかし、三角形の中には1辺の長さが分かれば面積が求められるものが存在します。
それはどんな三角形なのか3つの例を見ていきます。

1. 直角二等辺三角形

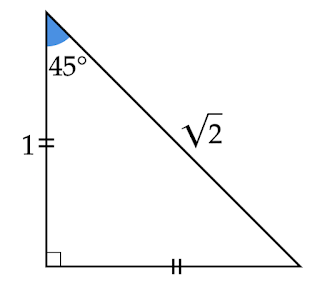
図1　直角二等辺三角形

　直角二等辺三角形は1つの角が直角であり、かつ直角をつくる2つの辺の長さが等しい三角形のことです。

直角をつくっている2辺がそのまま底辺と高さになり、これらは長さが等しいのでどちらか一方の長さがわかっていれば面積を求めることができます。

図2　斜辺と高さの関係

　また、斜辺の長さしかわかっていない場合は三角比から求めることもできますが、直角の頂点から斜辺に対して垂線を下ろすと合同な2つの直角二等辺三角形ができ、垂線の長さは斜辺の$\dfrac{1}{2}$となります。
したがって、斜辺の長さしかわかっていない場合でも面積も求めることができます。

その他、以下のように直角二等辺三角形の斜辺を1辺とする正方形を描くと、直角二等辺三角形の面積は正方形の$\dfrac{1}{4}$となることを利用して面積を求めることもできます。

図3　直角二等辺三角形の斜辺を1辺とする正方形

2. 有名角の直角三角形

　先程の直角二等辺三角形も有名角の直角三角形の1つであり、これに含まれる直角三角形はもう1つあります。

図4　$30°-60°-90°$の直角三角形

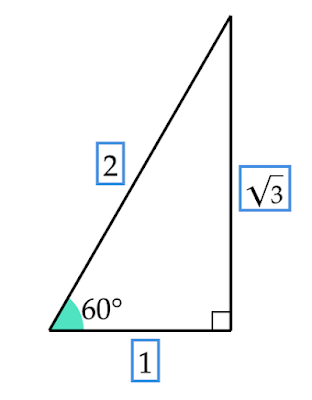
それは3つの角が$30°-60°-90°$の直角三角形です。この直角三角形の3辺の長さの比は$1:2:\sqrt{3}$であり、どれか1つでも辺の長さがわかれば他の辺の長さもわかるので面積を求めることができます。

また、この直角三角形は正三角形を半分に切ったものなので、正三角形の面積を求めるときにも利用することができます。

有名角の直角三角形に限定しましたが、3辺の比を知っている直角三角形であれば同様に1辺の長さから面積を求めることができます。

3. 底角が$75°$の二等辺三角形

図5　底角が75°の二等辺三角形

　底角が$75°$の二等辺三角形は一見1辺だけわかっても高さを知ることはできないように思えます。

図6　二等辺三角形に垂線を下ろす

しかし、底角の1つから対辺に垂線を下ろすと頂角は$30°$なので前述の直角三角形ができます。
垂線と等辺の長さは$1:2$となるため、等辺の長さがわかればそれを底辺としたときの高さを知ることができ、これらから面積を求めることができます。

　以上が1辺の長さがわかれば面積が求められる三角形の例です。

(2024/8)修正しました。