aベクトル-bベクトルはなぜこの向きなのか？

　$\vec{a}-\vec{b}$は$\vec{a}$の終点から$\vec{b}$の終点を指す矢印で表されます。なぜこの向きなのでしょうか？

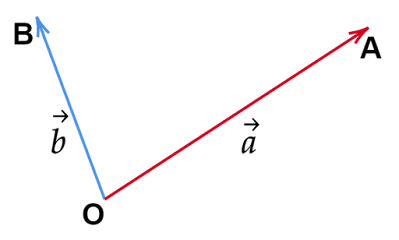
　点$\text{O}$を始点とする2つのベクトルのうち点$\text{A}$を終点とするベクトルを$\vec{a}$、点$\text{B}$を終点とするベクトルを$\vec{b}$とします。
ベクトル$\vec{a}-\vec{b}$をベクトルの和で考えると

$$\vec{a}-\vec{b}=\vec{a}+(-\vec{b})$$

と書けます。

$-\vec{b}$は$\vec{b}$と同じ大きさで逆向きのベクトルなので、これは点$\text{B}$を点$\text{O}$に関して対称移動した点$\text{B}'$を終点とするベクトルとなります。

したがって、$\vec{a}+(-\vec{b})$は$\vec{a}$と始点が点$\text{A}$になるよう平行移動した$-\vec{b}$を合成したベクトルなので、上図の点$\text{O}$を始点、点$\text{C}$を終点とするベクトルとなります。

すると四角形$\text{ABOC}$は$\vec{b}$と$-\vec{b}$は大きさが等しく平行なベクトルであることから平行四辺形であることがわかります。
このことから$\vec{a}-\vec{b}$は平行移動して始点を$\text{B}$、終点を$\text{A}$とするベクトルにもなるので、$\vec{a}$と$\vec{b}$の間に$\vec{a}-\vec{b}$を書き込むと上図のような大きさと向きをもつベクトルとなります。

各点に振ったアルファベットを使ってベクトルを表すと、

$$\vec{a}-\vec{b}=\vec{\text{OA}}-\vec{\text{OB}}=\vec{\text{BA}}$$

となり、点$\text{A, B}$の登場順が1つのベクトルで表したときとベクトルの差で表したときとで逆になります。