勾配伸び率とは何でしょうか？
その意味と3°刻みでの各角度における勾配伸び率がどうなるのかを調べてみました。
その意味と3°刻みでの各角度における勾配伸び率がどうなるのかを調べてみました。
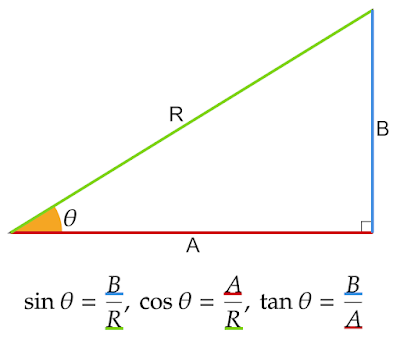
勾配伸び率とは、水平距離における斜面部分の距離の割合のことです。
例えば勾配伸び率$1.1$は水平方向に$1$m進んだとき、斜面上では$1.1$倍の$1.1$m進むことになるような傾斜であるということです。
\[(勾配伸び率)=\frac{R}{A}\]
で求められるので、$\dfrac{1}{\cosθ}=\secθ$に等しくなります。
斜面距離、直角三角形で言う斜辺の長さが最も長いので勾配伸び率は必ず$1$以上となります。
また、勾配率は$\tanθ$に等しいので、三角比の相互関係
\[1+\tan^2\theta=\frac{1}{\cos^2\theta}\]
より、勾配伸び率は
\[(勾配伸び率)=\sqrt{1+(勾配率)^2}\]
でも求めることができることがわかります。
$0°\leqqθ\leqq90°$のときの勾配伸び率の値がどうなるのかを$3°$刻みで求めると以下のようになります。
| 角度$θ$ | 勾配率 $tanθ$ |
$\cosθ$ | 勾配伸び率 |
|---|---|---|---|
| $0°$ | $0.000$ | $1.00000$ | $1.000$ |
| $3°$ | $0.052$ | $0.99863$ | $1.001$ |
| $6°$ | $0.105$ | $0.99452$ | $1.006$ |
| $9°$ | $0.158$ | $0.98769$ | $1.012$ |
| $12°$ | $0.213$ | $0.97815$ | $1.022$ |
| $15°$ | $0.268$ | $0.96593$ | $1.035$ |
| $18°$ | $0.325$ | $0.95106$ | $1.051$ |
| $21°$ | $0.384$ | $0.93358$ | $1.071$ |
| $24°$ | $0.445$ | $0.91355$ | $1.095$ |
| $27°$ | $0.510$ | $0.89100$ | $1.122$ |
| $30°$ | $0.577$ | $0.86603$ | $1.154$ |
| $33°$ | $0.649$ | $0.83867$ | $1.192$ |
| $36°$ | $0.727$ | $0.80902$ | $1.236$ |
| $39°$ | $0.810$ | $0.77715$ | $1.287$ |
| $42°$ | $0.900$ | $0.74314$ | $1.346$ |
| $45°$ | $1.000$ | $0.70701$ | $1.414$ |
| $48°$ | $1.111$ | $0.66913$ | $1.494$ |
| $51°$ | $1.235$ | $0.62932$ | $1.589$ |
| $54°$ | $1.376$ | $0.58779$ | $1.701$ |
| $57°$ | $1.540$ | $0.54464$ | $1.836$ |
| $60°$ | $1.732$ | $0.50000$ | $2.000$ |
| $63°$ | $1.963$ | $0.45399$ | $2.202$ |
| $66°$ | $2.246$ | $0.40674$ | $2.459$ |
| $69°$ | $2.605$ | $0.35836$ | $2.790$ |
| $72°$ | $3.078$ | $0.30902$ | $3.236$ |
| $75°$ | $3.732$ | $0.25882$ | $3.864$ |
| $78°$ | $4.705$ | $0.20791$ | $4.810$ |
| $81°$ | $6.314$ | $0.15643$ | $6.392$ |
| $84°$ | $9.514$ | $0.10453$ | $9.567$ |
| $87°$ | $19.081$ | $0.05234$ | $19.107$ |
| $90°$ | - | - | - |
$θ=90°$のとき、勾配率の値がないこと、分母となる$\cosθ$が$0$となることから勾配伸び率の値もないことがわかります。
Share:
