三角関数の読み方 ②単位円の利用

　$90°$より大きい角度のときの三角関数$\sinθ,\cosθ,\tanθ$の値はどうやって求めるのでしょうか？
単位円をもちいて扱える角度の範囲を拡張します。

単位円による定義

　任意の$θ$における$\sinθ,\cosθ,\tanθ$の定義には半径$1$の円（単位円）を利用します。

単位円を座標平面上に原点を中心として描きます。

ここにx軸の正の部分と反時計回りを正の方向として$θ$の角をなす半径を引きます。（すなわち、この定義においてもちいる角度は一般角で、$θ$の角をなす半径は動径でもあります。）

関連：一般角とは？

その半径の円周上の端点の座標を$\mathbf(\cosθ,\sinθ)$、半径を延長した直線の傾きを$\mathbf\tanθ$とします。

これらがどんな値を持つのかは三角比を利用することで求められます。

関連：三角関数の読み方　①三角比の読み方

$0°<θ<90°$のとき

　$0°<θ<90°$のとき、半径の円周上の端点は$x>0$かつ$y>0$の領域内にあります。この領域を第1象限といいます。

半径の円周上の端点からx軸へ垂線をおろし、半径とx軸、垂線で囲まれた直角三角形をつくります。

すると、直角三角形の三角比よりx軸上の辺の長さは$\mathbf{\cosθ}$、x軸に対する垂線からなる辺の長さは$\mathbf{\sinθ}$となります。

また、原点と点$(\cosθ,\sinθ)$を通る直線の傾きより$\tanθ$は

$$\tan\theta=\frac{\sin\theta}{\cos\theta}$$

となります。

さらに$\tanθ$は半径の延長と直線$x=1$の交点のy座標としても求められます。

これは原点を通る直線においては$x=1$における点のy座標がそのまま傾きの値として表れるためです。

　このように第一象限における$\sinθ,\cosθ,\tanθ$の値は三角比と全く同じものとなります。

$90°<θ<180°$のとき

　$90°<θ<180°$のとき、半径の円周上の端点は$x<0,y>0$の領域内にあります。この領域を第2象限といいます。
半径の円周上の端点の座標は第1象限のときと同様この点からx軸へ垂線をおろして半径とx軸、垂線で囲まれた直角三角形をもちいて求めます。

この直角三角形の原点を頂点とする内角の大きさは$180°-θ$となります。

したがって、三角比よりx軸上にある辺の長さは$\cos(180°-θ)$、垂線からなる辺の長さは$\sin(180°-θ)$となります。

すると、半径の円周上の端点$(\cosθ,\sinθ)$は領域$x<0,y>0$内にあるから

$$\begin{align*}\cos\theta&=-\cos(180°-\theta)\\[1em]\sin\theta&=\sin(180°-\theta)\end{align*}$$

であることがわかります。

また、$\tanθ$は

$$\begin{align*}\tan\theta&=\frac{\sin\theta}{\cos\theta}\\[0.5em]&=\frac{\sin(180°-\theta)}{-\cos(180°-\theta)}\\[0.5em]&=-\frac{\sin(180°-\theta)}{\cos(180°-\theta)}\\[0.5em]&=-\tan(180°-\theta)\end{align*}$$

となります。

　第2象限において$180°-θ$は鋭角なので、$\sin(180°-θ),\cos(180°-θ),\tan(180°-θ)$は第1象限における三角関数の値と同じものとなります。

したがって、上で得られた

$$\begin{equation}\begin{aligned}\begin{cases}\sin\theta&=\sin(180°-\theta)\\[0.5em]\cos\theta&=-\cos(180°-\theta)\\[0.5em]\tan\theta&=-\tan(180°-\theta)\end{cases}\\ &(90°<\theta<180°)\end{aligned}\end{equation}$$

は第1象限と第2象限の三角関数の関係を表す式となります。

これを利用して例えば$\cos120°$の値を求めたいときは

$$\begin{align*}\cos120°&=\cos(180°-60°)\\[0.5em]&=-\cos60°\end{align*}$$

と変換でき、$30°-60°-90°$の直角三角形における三角比より$\cos60°=\dfrac{1}{2}$なので
$$\cos120°=-\frac{1}{2}$$
と導き出すことができます。

$180°<θ<270°$のとき

　$180°<θ<270°$のとき、半径の円周上の端点は$x<0,y<0$の領域内にあります。この領域を第3象限といいます。

半径の円周上の端点の座標は第1象限のときと同様この点からx軸へ垂線をおろして半径とx軸、垂線で囲まれた直角三角形をもちいて求めます。

この直角三角形の原点を頂点とする内角の大きさは$θ-180°$となります。
したがって、三角比よりx軸上にある辺の長さは$\cos(θ-180°)$、垂線からなる辺の長さは$\sin(θ-180°)$となります。

すると、半径の円周上の端点$(\cosθ,\sinθ)$は領域$x<0,y<0$内にあるから

$$\begin{align*}\cos\theta&=-\cos(\theta-180°)\\[1em]\sin\theta&=-\sin(\theta-180°)\end{align*}$$

であることがわかります。

また、$\tanθ$は

$$\begin{align*}\tan\theta&=\frac{\sin\theta}{\cos\theta}\\[0.5em]&=\frac{-\sin(\theta-180°)}{-\cos(\theta-180°)}\\[0.5em]&=\frac{\sin(\theta-180°)}{\cos(\theta-180°)}\\[0.5em]&=\tan(\theta-180°)\end{align*}$$

となります。

　第3象限において$θ-180°$は鋭角なので、$\sin(θ-180°),\cos(θ-180°),\tan(θ-180°)$は第1象限における三角関数の値と同じものとなります。

したがって、上で得られた

$$\begin{equation}\begin{aligned}\begin{cases}\sin\theta&=-\sin(\theta-180°)\\[0.5em]\cos\theta&=-\cos(\theta-180°)\\[0.5em]\tan\theta&=-\tan(\theta-180°)\end{cases}\\ &(180°<\theta<270°)\end{aligned}\end{equation}$$

は第1象限と第3象限の三角関数の関係を表す式となります。

これを利用して例えば$\sin225°$の値を求めたいときは

$$\begin{align*}\sin225°&=\sin(180°+45°)\\[0.5em]&=-\sin45°\end{align*}$$

と変換できるため、$45°-45°-90°$の直角三角形の三角比より$\sin45°=\dfrac{\sqrt{2}}{2}$なので
$$\sin225°=-\frac{\sqrt{2}}{2}$$
と導き出すことができます。

$270°<θ<360°$のとき

　$270°<θ<360°$のとき、半径の円周上の端点は$x>0,y<0$の領域内にあります。この領域を第4象限といいます。

半径の円周上の端点の座標は第1象限のときと同様この点からx軸へ垂線をおろして半径とx軸、垂線で囲まれた直角三角形をもちいて求めます。

この直角三角形の原点を頂点とする内角の大きさは$360°-θ$となります。

したがって、三角比よりx軸上にある辺の長さは$\cos(360°-θ)$、垂線からなる辺の長さは$\sin(360°-θ)$となります。

すると、半径の円周上の端点$(\cosθ,\sinθ)$は領域$x>0,y<0$内にあるから

$$\begin{align*}\cos\theta&=\cos(360°-\theta)\\[1em]\sin\theta&=-\sin(360°-\theta)\end{align*}$$

であることがわかります。

また、$\tanθ$は

$$\begin{align*}\tan\theta&=\frac{\sin\theta}{\cos\theta}\\[0.5em]&=\frac{-\sin(360°-\theta)}{\cos(360°-\theta)}\\[0.5em]&=-\frac{\sin(360°-\theta)}{\cos(360°-\theta)}\\[0.5em]&=\tan(360°-\theta)\end{align*}$$

となります。

　第4象限において$360°-θ$は鋭角なので、$\sin(360°-θ),\cos(360°-θ),\tan(360°-θ)$は第1象限における三角関数の値と同じものとなります。

したがって、上で得られた

$$\begin{equation}\begin{aligned}\begin{cases}\sin\theta&=-\sin(360°-\theta)\\[0.5em]\cos\theta&=-\cos(360°-\theta)\\[0.5em]\tan\theta&=-\tan(360°-\theta)\end{cases}\\ &(270°<\theta<360°)\end{aligned}\end{equation}$$

は第1象限と第4象限の三角関数の関係を表す式となります。

これを利用して例えば$\tan300°$の値を求めたいときは

$$\begin{align*}\tan300°&=\tan(360°-60°)\\[0.5em]&=-\tan60°\end{align*}$$

と変換できるため、$30°-60°-90°$の直角三角形の三角比より$\tan60°=\sqrt{3}$なので
$$\tan300°=-\sqrt{3}$$
と導き出すことができます。

$θ=0°,90°,180°,270°,360°$のとき

　$θ=0°,90°,180°,270°,360°$のときは直角三角形をつくることはできませんが、それぞれの場合の半径の円周上の端点の座標はすぐにわかるので、$\sinθ,\cosθ,\tanθ$の値を求められます。

$θ=0°$のとき

　半径の円周上の端点の座標は$(1,0)$なので

$$\sin0°=0,\cos0°=1$$

$\tan0°$は

$$\begin{align*}\tan0°&=\frac{\sin0°}{\cos0°}\\[0.5em]&=\frac{0}{1}\\[0.5em]&=0\end{align*}$$

となります。

$θ=90°$のとき

　半径の円周上の端点の座標は$(0,1)$なので

$$\sin90°=1,\cos90°=0$$

$\tan90°$は

$$\begin{align*}\tan90°&=\frac{\sin90°}{\cos90°}\\[0.5em]&=\frac{1}{0}\end{align*}$$

より、分母が$0$となるため定義できません。

$θ=180°$のとき

　半径の円周上の端点の座標は$(-1,0)$なので

$$\sin180°=0,\cos180°=-1$$

$\tan180°$は

$$\begin{align*}\tan180°&=\frac{\sin180°}{\cos180°}\\[0.5em]&=\frac{0}{-1}\\[0.5em]&=0\end{align*}$$

となります。

$θ=270°$のとき

　半径の円周上の端点の座標は$(0,-1)$なので

$$\sin270°=-1,\cos270°=0$$

$\tan270°$は

$$\begin{align*}\tan270°&=\frac{\sin270°}{\cos270°}\\[0.5em]&=\frac{-1}{0}\end{align*}$$

より、分母が$0$となるため定義できません。

$θ=360°$のとき

　半径は$θ=0°$のときと同じ位置であるため

$$\begin{align*}\sin360°&=0\\[1em]\cos360°&=1\\[1em]\tan360°&=0\end{align*}$$

となります。

$θ=0°,180°,360°$のとき半径はx軸と重なっています。この半径を延長した直線の傾きは$0$なので$\tan$の値も$0$となります。

$θ=90°,270°$のとき半径はy軸と重なっています。この半径を延長した直線の傾きは定義できないので、$\tan$の値も定義できません。
これはy軸と重なった半径は直線$x=1$と平行なため、どれだけ延長しても交点をもち得ず、そのy座標も存在しないことからもわかります。

　$θ$が$0°～360°$以外の角度をとるときの三角関数も定義することができます。

$θ>360°$のとき

　$360°$回転すると元の位置に戻ってくるので、ある角度$θ$に$360°×n$（$n:$整数）を加えても引いても三角関数の値は変わりません。

すなわち以下が成り立ちます。

$$\begin{align*}\sin\theta&=\sin(\theta\pm360°\times n)\\[1em]\cos\theta&=\cos(\theta\pm360°\times n)\\[1em]\tan\theta&=\tan(\theta\pm360°\times n)\\ &&(n:自然数)\end{align*}$$

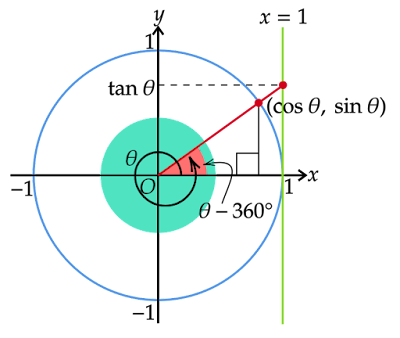
$θ>360°$のときは$360°×n$を引き、$0°\leqqθ-360°×n\leqq360°$となるように$n$を決めれば、これまでのいずれかの$θ$の場合に置き換えて考えることができます。（上図は$360°<θ<720°$の場合）

例えば$\tan480°$の値を求めたい場合は以下のようになります。

$$\tan480°=\tan(480°-360°×n)$$

が成り立ち、$n=1$を代入すると

$$\begin{align*}\tan480°&=\tan(480°-360°)\\[0.5em]&=\tan120°\end{align*}$$

となります。
$90°<θ<180°$の場合より

$$\begin{align*}\tan120°&=\tan(180°-60°)\\[0.5em]&=-\tan60°\\[0.5em]&=-\sqrt{3}\end{align*}$$

したがって、

$$\tan480°=-\sqrt{3}$$

となります。

$θ<0°$のとき

　$θ$は負の角度をとる場合もあります。これを負角といいます。

$θ>360°$のときは$360°×n$（$n:$自然数）を引きましたが、$θ<0°$のときは$360°×n$を加えます。

$θ>360°$のときと同様に$0°\leqqθ+360°×n\leqq360°$となるように$n$を決めれば、これまでのいずれかの$θ$の場合に置き換えて考えることができます。（上図は$-360°<θ<0°$の場合）

例えば$\sin(-60°)$の値を求めたい場合は以下のようになります。

$$\sin(-60°)=\sin(-60°+360°×n)$$

が成り立ち、$n=1$を代入すれば

$$\begin{align*}\sin(-60°)=\sin(-60°+360°)\\[0.5em]&=\sin300°\end{align*}$$

となります。
$270°<θ<360°$の場合より

$$\begin{align*}\sin300°&=\sin(360°-60°)\\[0.5em]&=-\sin60°\\[0.5em]&=-\frac{\sqrt{3}}{2}\end{align*}$$

したがって、

$$\sin(-60°)=-\frac{\sqrt{3}}{2}$$

となります。

　以上のように、あらゆる角度の三角関数の値は、その角度のとき単位円周上の点がどこにあるのかを考えることで求めることができます。

三角関数を含む方程式、不等式は単位円を活用して解きます。

　「三角関数の読み方　①三角比の読み方」でほんの少しだけ触れましたが、三角関数と三角比の違いは上図のようになります。

直角三角形または単位円による定義からなる角度に応じた値を返す上図でとりあげた$\sinθ$や$\cosθ,\tanθ$のような関数が三角関数、三角関数が返す値のうち$0°<θ<90°$の角度から返された値が三角比です。

関連：三角関数の読み方　①三角比の読み方

$(1),(2),(3)$は任意の$θ$においても成り立ちます。
関連：$-θ,90°±θ,180°±θ,270°±θ$の三角関数