三角関数を含む不等式を解く ~ 数学について考えてみる

2022年3月8日

三角関数を含む不等式を解く

PLUMBAGO

「

0 ≦ θ ≦ 2 π

$0\leqqθ\leqq2\pi$ のとき、以下の不等式を解け。

(1) $\large\sinθ\geqq\frac{\sqrt{2}}{2}$

(2)

tan θ < \sqrt{3}

$\large\tanθ<\sqrt{3}$ 」

このような問題はどのように解けばよいでしょうか？

(1) $\sinθ\geqq\frac{\sqrt{2}}{2}$

　まずは不等号を等号に置き換えたときの

θ

$θ$ を求めます。

sin θ = \frac{\sqrt{2}}{2}

$\sinθ=\frac{\sqrt{2}}{2}$

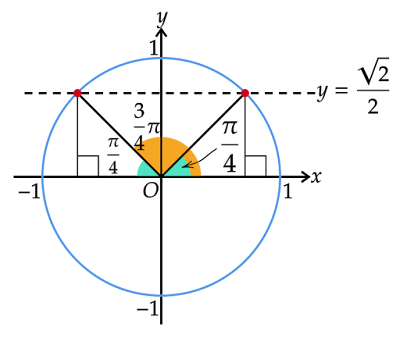
この方程式が成り立つときを単位円で考えると以下のようになります。

sinθ=√2/2

このことから

θ = \frac{π}{4}, \frac{3 π}{4}

$θ=\dfrac{\pi}{4},\dfrac{3\pi}{4}$ であることがわかります。

sinθ≧√2/2

そして問題の不等式は

sin θ

$\sinθ$ が

\frac{\sqrt{2}}{2}

$\dfrac{\sqrt{2}}{2}$ 以上の値をもつことを意味しており、これに当てはまるのは動径の単位円上の端点が上図の赤色の弧上にあるときとなります。該当する動径の表す角度がこの不等式の解となります。

したがって解は

\frac{π}{4} ≦ θ ≦ \frac{3 π}{4}

$\frac{\pi}{4}\leqqθ\leqq\frac{3\pi}{4}$

となります。

(2) $\tanθ<\sqrt{3}$

　

(1)

$(1)$ と同様

tan θ = \sqrt{3}

$\tanθ=\sqrt{3}$

を解きます。

tanθ=√3

この方程式が成り立つときを単位円で考えると上図のようになるので、

θ = \frac{π}{3}, \frac{4 π}{3}

$θ=\frac{\pi}{3},\frac{4\pi}{3}$ となります。

tanθ<√3

そして問題の不等式

tan θ

$\tanθ$ が

\sqrt{3}

$\sqrt{3}$ 未満の値をもつことを意味しており、これに当てはまるのは上図の直線

x = 1

$x=1$ 上の緑の線の部分を通るような動径のとき、すなわち動径の単位円上の端点が赤い弧上（ただし、白丸は含まない）にあるときとなります。

$θ=\dfrac{\pi}{2}$ を含まないことについてですが、 $\tanθ$ の値について考えると $0\leqqθ\leqq2\pi$ において $θ=\dfrac{\pi}{2}、\dfrac{3\pi}{2}$ のときは値がありません。
$tanθ$ の値のないときの $θ$ は範囲に含むことができないので、 $\tanθ$ に限り $0\leqqθ\leqq2\pi$ は $0\leqqθ<\dfrac{\pi}{2},\dfrac{\pi}{2}<θ<\dfrac{3\pi}{2},\dfrac{3\pi}{2}<θ\leqq2\pi$ と $θ=\dfrac{\pi}{2}、\dfrac{3\pi}{2}$ を除いてできる3つの範囲に分割して考えることになります。

したがって、解は

0 ≦ θ < \frac{π}{3}, \frac{π}{2} < θ < \frac{4 π}{3}

$0\leqqθ<\frac{\pi}{3},\frac{\pi}{2}<θ<\frac{4\pi}{3}$

となります。

Share: