不等式と必要条件、十分条件

「次の条件が成り立つような$a,b$の範囲を求めよ。

(1)$2x+a>0$であることが$x^2-10x+21\leqq0$であるための必要条件
(2)$x^2-10x+21>0$であることが$|x-b|-2>0$であるための十分条件」

このような問題はどのように解けばよいでしょうか？

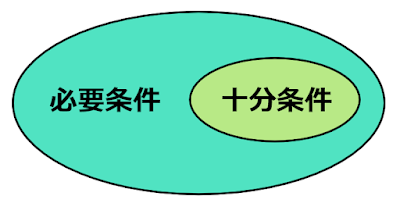
　まずは必要条件、十分条件について考えます。

必要条件、十分条件の関係は下図のようになります。

このように十分条件となる不等式は必要条件となる不等式の中に含まれることになります。

(1)

　それぞれの不等式を解きます。

$$\begin{align*}2x+a&>0\\ 2x&>-a\\ x&>-\frac{a}{2}&...(i)\\ \\ x^2-10x+21&\leqq0\\ (x-3)(x-7)&\leqq0\\ 3\leqq&x\leqq7&...(ii)\end{align*}$$

(i)が必要条件、(ii)が十分条件となるので、これらの範囲が下図のようにならなければ成り立ちません。

したがって、

$$\begin{align*}-\frac{a}{2}&<3\\ \\ -a&<6\\ \\ a&>-6\end{align*}$$

となります。

(2)

　それぞれの不等式を解きます。

$$\begin{align*}x^2-10x+21&>0\\ (x-3)(x-7)&>0\\ x<3,&7<x&...(i)\\ \\ |x-b|-2&>0\\ I. x>b\qquad\qquad&\\ x-b-2&>0\\ x&>b+2\\ II. x<b\qquad\qquad&\\ -(x-b)-2&>0\\ -x+b-2&>0\\ -x&>-b+2\\ x&<b-2\\ \\ \therefore x<b-2,&b+2<x&...(ii)\end{align*}$$

(i)が十分条件、(ii)が必要条件なので、これらの範囲が以下のようにならなければ成り立ちません。

したがって、$x<b-2$が$x<3$の必要条件となっていることと、$x>b+2$が$x>7$の必要条件となっていることが同時に満たされていれば良いので

$$\begin{align*}I.\qquad\qquad&\\ b-2&\geqq3\\ b&\geqq5&...(iii)\\ II.\qquad\qquad&\\ b+2&\leqq7\\ b&\leqq5&...(iv)\end{align*}$$

(iii)かつ(iv)より

$$b=5$$

となります。

(ii)に代入すると

$$x<3,7<x$$

となり、(i)と一致します。このことから$x^2-10x+21>0$と$|x-5|-2>0$は必要十分条件であることがわかります。