y=x^2とy=2^xの3つ目の共有点をニュートン法で探してみる

　$y=x^2$と$y=2^x$の共有点のx座標は

$$x^2=2^x$$

という方程式を解くことで求めることができます。

　両辺の対数をとると

$$\begin{align*}\log x^2&=\log2^x\\[0.5em] 2\log x&=x\log2\\[0.5em] \frac{\log x}{x}&=\frac{\log2}{2}\end{align*}$$

両辺を比較して$x=2$。

また、$4=2^2=2×2$となることに着目すると

$$\begin{align*}\frac{\log4}{4}&=\frac{\log2^2}{2×2}\\[0.5em] &=\frac{2\log2}{2×2}\\[0.5em] &=\frac{\log2}{2}\end{align*}$$

であるから$x=4$、よって解は$x=2,4$となります。

しかし、グラフを描いてみると

図1　$y=x^2$と$y=2^x$のグラフ

$x=2,4$の2点以外にもう1点、$x<0$の範囲にも共有点が存在します。しかし、この共有点のx座標を求めるのは容易ではありません。
なのでこの共有点のx座標の近似値をニュートン法をもちいて求めてみようと思います。

図2　接線のx切片は接点よりx軸との共有点に近い

　ニュートン法とは、関数のグラフとx軸との共有点近傍のx座標$x_n$より$x_n$における接線のx切片$x_{n+1}$のほうが共有点のx座標により近いことを利用した実数解の近似値を求める方法のことです。
x切片を次の接点のx座標として繰り返し接線のx切片を求めていくことで共有点のx座標、すなわち実数解に収束していきます。

　$y=f(x)$のx軸の共有点の付近の接点$\bigl(x_n,f(x_n)\bigr)$の接線の方程式は

$$y-f(x_n)=f'(x_n)(x-x_n)$$

となります。この接線のx切片を$x_{n+1}$とすれば点$(x_{n+1},0)$を通るので

$$0-f(x_n)=f'(x_n)(x_{n+1}-x_n)$$

したがって、$x_{n+1}$は

$$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}\qquad(ただし、f'(x_n)\neq0)$$

と表されます。

ちなみに上の式の$f(x)$と$f'(x)$は、$y=x^2$と$y=2^x$の3つ目の共有点のx座標（負の実数解）を求めるための方程式の変形$x^2-2^x=0$より

$$f(x)=x^2-2^x$$

と、その導関数

$$f'(x)=2x-\log_e2\cdot2^x$$

となるので、

$$x_{n+1}=x_n-\frac{{x_n}^2-2^{x_n}}{2{x_n}-\log_e2\cdot2^{x_n}}$$

とも書けます。

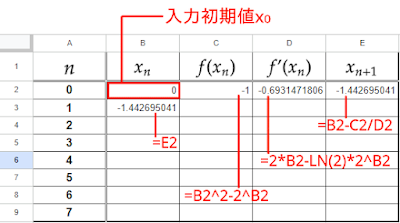
$x_n$に負の実数解に近い$x$の値として$x_0=0$を設定しGoogleスプレッドシートで計算します。

セルへの入力例は以下のとおりです。（残りのセルは上のセルからオートフィル機能で埋めます。）

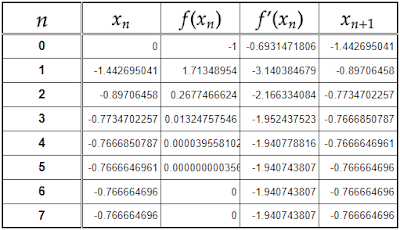
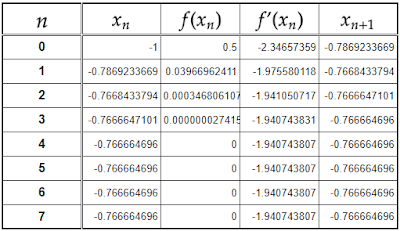
すると

$n=5$で収束し$x=-0.766664696$という値を得ることができます。

この値を$y=x^2$と$y=2^x$に代入してみると

$$\begin{align*}(-0.766664696)^2&≒0.587774756\\[0.5em] 2^{-0.766664696}&≒0.587774756\end{align*}$$

同様の値を得ることがわかります。

$x_0=-1$としても同様に$x=-0.766664696$に収束します。

　ただし、これはあくまで近似解です。

上の結果では値が収束しているようですが、Googleスプレッドシートで計算で扱えるのは15桁までのようで、その限られた桁数で計算していたため値が収束しているように見えているようです。

なので、値の収束=真の解を得たというわけではありませんが、十分有用な値であると思います。

微分と表計算ソフトの知識さえあれば簡単に近似解を求められるので、試してみてください。

外部リンク：ニュートン法 - Wikipedia