直方体のねじれの位置にある辺

「図の直方体$\text{ABCD-EFGH}$において辺$\text{AB}$とねじれの位置にある辺を全て挙げよ。」

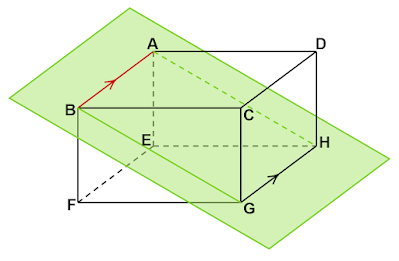
　ねじれの位置にある辺を挙げる前に、交わる辺と平行な辺がどれなのかを挙げてみます。

交わる辺

　交わる辺には以下のような特徴があります。

• 2つの辺は同一平面上にある。
• 2つの辺が1つの共有点をもつ。

共有点とは異なる線が共通してもっている点のことです。この場合においては頂点のこととなります。辺$\text{AB}$と交わっている辺は$\text{AD, AE, BC, BF}$の4つです。それ以外の辺は辺$\text{AB}$と頂点をもたないので交わっていません。

辺$\text{AB, AD, BC}$は面$\text{ABCD}$を同一平面としています。辺$\text{AB, AE, BF}$も同様に面$\text{ABEF}$を同一平面としています。

したがって、辺$\text{AB}$と交わる辺は$\text{AD, AE, BC, BF}$の4つであることがわかります。

直方体の交わる辺はすべて直交しているので垂直な辺でもあります。

ちなみに$\text{AB}$に垂直な辺は先の4辺に加え辺$\text{CG, DH, EH, FG}$が当てはまります。
垂直な辺とは平行移動すれば直交する辺のことで、辺$\text{CG, DH, EH, FG}$に平行な辺のことであるともいえます。

平行な辺

　互いに平行な辺には以下のような特徴があります。

• 2つの辺は同一平面上にある。
• 2つの辺を延長しても共有点がない。

前述の辺$\text{AB}$を含む平面、面$\text{ABCD}$と面$\text{ABEF}$の中で交わっていない辺は$\text{CD, EF}$です。
面$\text{ABCD}$と面$\text{ABEF}$は長方形であるから辺$\text{AB}$の対辺である辺$\text{CD, EF}$は平行であることがわかります。

辺$\text{GH}$も辺$\text{AB}$に平行です。順を追って確かめます。

辺$\text{AB}$は辺$\text{AD, AE}$と垂直であるから辺$\text{AD, AE}$を含む面$\text{ADHE}$と辺$\text{AB}$は垂直です。
また、辺$\text{GH}$は辺$\text{DH, EH}$と垂直であるから辺$\text{DH, EH}$を含む面$\text{ADHE}$と辺$\text{GH}$は垂直です。

したがって、面$\text{ADHE}$に対し辺$\text{AB, GH}$はともに垂直なので、辺$\text{AB}$と辺$\text{GH}$は平行であることがわかります。

このことから辺$\text{GH}$も辺$\text{AB}$と同一平面にあることがわかります。直方体$\text{ABCD-EFGH}$をまっすぐ切断すると、辺$\text{AB}$と辺$\text{GH}$を含んだ平面ができることがあることはよく知られていると思います。

もしくは面$\text{CDHG}$において$\text{CD}//\text{HG}$であるから$\text{AB}//\text{CD}//\text{HG}$、すなわち$\text{AB}//\text{HG}$であるというように考えることもできます。

以上より辺$\text{AB}$と平行な辺は$\text{CD, EF, HG}$の3つであることがわかります。

ねじれの位置にある辺

　ねじれの位置にある辺は交わる辺、平行な辺のどちらにも当てはまらない辺のことを指します。

特に両者に共通する「同一平面上にある」という特徴に当てはまらないものを指します。

したがって、交わらず平行でもない辺である辺$\text{CG, DH, EH, FG}$の4つがねじれの位置にある辺となります。