三垂線の定理とは？

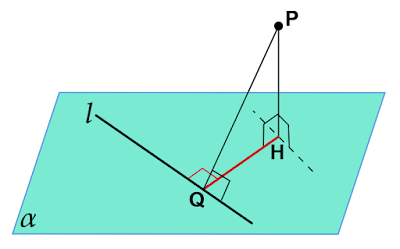
　平面$α$上にない点$\text{P}$から平面$α$へ垂線をおろし、その足を$\text{H}$とします。
点$\text{H}$から平面$α$上の直線$l$へ垂線をおろし、その足を$\text{Q}$とします。

このとき、直線$\text{PQ}$は直線$l$に垂直となります。これを三垂線の定理といいます。

この定理は命題の形では

\[\large \text{PH}\perp\alphaかつ \text{QH}\perp l\Rightarrow \text{PQ}\perp l\]

のように書きます。

なぜこれが成り立つのでしょうか？

　平面に垂直な直線は、平面上のどの直線とも垂直となります。
したがって、平面$α$の垂線$\text{PH}$は直線$l$とも垂直です。

ここで直線$\text{PH}$と$\text{QH}$を含む平面$\text{PQH}$を考えると、$\text{PH}\perp l$かつ$\text{QH}\perp l$より直線$l$は平面$\text{PQH}$に垂直であることがわかります。

関連：直線と平面が垂直であるとは？

よって、直線$\text{PH, QH}$と同様に平面$\text{PQH}$上にある直線$\text{PQ}$と直線$l$も垂直であることがわかります。

三垂線の定理の系

　三垂線の定理には派生（系）があり、それらは以下のようなものです。

系1：平面$α$上にない点$\text{P}$から平面$α$上の直線$l$に垂線を引き、その足を$\text{Q}$とします。
また、点$\text{P}$から平面$α$へ垂線を下ろし、その足を$\text{H}$とします。

このとき、直線$\text{QH}$は直線$l$に垂直となります。

これは命題の形で

\[\text{PQ}\perp lかつ \text{PH}\perp\alpha\Rightarrow \text{QH}\perp l\]

と書きます。

系2：平面$α$上にない点$\text{P}$から平面$α$上の直線$l$に垂線を引き、その足を$\text{Q}$とします。
また、直線$l$への垂線の足が$\text{Q}$となるような点$\text{H}$を$\text{PH}\perp \text{QH}$が成り立つように平面$α$上にとります。

このとき、直線$\text{PH}$は平面$α$に垂直となります。

これは命題の形で

\[\text{PQ}\perp lかつ \text{QH}\perp lかつ \text{PH}\perp \text{QH}\Rightarrow \text{PH}\perp\alpha\]

と書きます。

これらが成り立つことも確かめてみます。

系1

　$\text{PH}\perp α$より、直線$\text{PH}$は平面$α$上のどの直線とも垂直です。
したがって、直線$\text{PH}$は平面$α$上の直線$l$と垂直であることがわかります。

$\text{PQ}\perp l$かつ$\text{PH}\perp l$より、直線$l$は平面$\text{PQH}$に垂直であることがわかります。
よって、直線$l$は平面$\text{PQH}$上の直線$\text{QH}$とも垂直となります。

系2

　$\text{PQ}\perp l$かつ$\text{QH}\perp l$より、直線$l$は平面$\text{PQH}$と垂直であることがわかります。
したがって、直線$l$は平面$\text{PQH}$上の直線$\text{PH}$とも垂直です。

$\text{PH}\perp l$かつ$\text{PH}\perp \text{QH}$より、直線$\text{PH}$は平面$α$に垂直であることがわかります。

関連：直線と平面が垂直であるとは？