ベクトルの内積を表す2式 ~ 数学について考えてみる

2022年3月9日

ベクトルの内積を表す2式

PLUMBAGO

\vec{A} = (a_{1}, a_{2}), \vec{B} = (b_{1}, b_{2})

$\vec{\text{A}}=(a_1,a_2),\vec{\text{B}}=(b_1,b_2)$ の2つのベクトルのなす角がθであるとき内積を表す式は

\begin{aligned} \vec{A} \cdot \vec{B} = | \vec{A} | | \vec{B} | \cos θ \\ \vec{A} \cdot \vec{B} = a_{1} b_{1} + a_{2} b_{2} \end{aligned}

$\begin{align*}\vec{\text{A}}\cdot\vec{\text{B}}=|\vec{\text{A}}||\vec{\text{B}}|\cosθ\\[1em]\vec{\text{A}}\cdot\vec{\text{B}}=a_1b_1+a_2b_2\end{align*}$

の2式あります。

この2式がどちらも内積を表していることを確かめてみます。

　内積を定義する式

\vec{A} \cdot \vec{B} = | \vec{A} | | \vec{B} | \cos θ

$\vec{\text{A}}\cdot\vec{\text{B}}=|\vec{\text{A}}||\vec{\text{B}}|\cosθ$

から

\vec{A} \cdot \vec{B} = a_{1} b_{1} + a_{2} b_{2}

$\vec{\text{A}}\cdot\vec{\text{B}}=a_1b_1+a_2b_2$ が導けることを確かめます。

\vec{A}, \vec{B}

$\vec{\text{A}},\vec{\text{B}}$ それぞれのベクトルの大きさは

\begin{aligned} | \vec{A} | & = \sqrt{{a_{1}}^{2} + {a_{2}}^{2}} \\ | \vec{B} | & = \sqrt{{b_{1}}^{2} + {b_{2}}^{2}} \end{aligned}

$\begin{align*}|\vec{\text{A}}|&=\sqrt{{a_1}^2+{a_2}^2}\\[0.5em]|\vec{\text{B}}|&=\sqrt{{b_1}^2+{b_2}^2}\end{align*}$

となります。

　次にベクトルの成分を使ってどうやって

\cos θ

$\cosθ$ を表すかを考えます。

ここで、

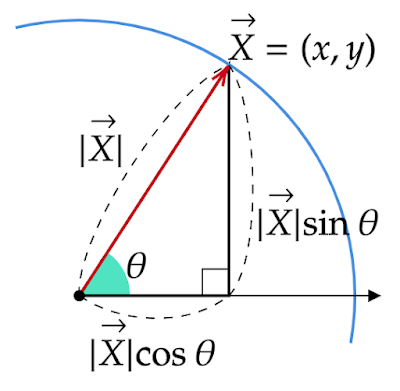
\vec{X} = (x, y)

$\vec{\text{X}}=(x,y)$ というベクトルを考え、このベクトルの始点を中心とし、

| \vec{X} |

$|\vec{\text{X}}|$ を半径とする円を考えます。
円の中心からx軸の正の方向にのびる直線と

\vec{X}

$\vec{\text{X}}$ とのなす角を

θ

$θ$ としたとき、三角関数の値を求めるときと同様にすれば

{\begin{cases} x = | \vec{X} | \cos θ \\ y = | \vec{X} | \sin θ \end{cases}

$\begin{cases}x=|\vec{\text{X}}|\cosθ\\[0.5em]y=|\vec{\text{X}}|\sinθ\end{cases}$

となります。

このことから

{\begin{cases} \cos θ = \frac{x}{| \vec{X} |} = \frac{x}{\sqrt{x^{2} + y^{2}}} \\ \sin θ = \frac{y}{| \vec{X} |} = \frac{y}{\sqrt{x^{2} + y^{2}}} \end{cases}

$\begin{cases}\cosθ=\frac{x}{|\vec{\text{X}}|}=\frac{x}{\sqrt{x^2+y^2}}\\[0.5em]\sinθ=\frac{y}{|\vec{\text{X}}|}=\frac{y}{\sqrt{x^2+y^2}}\end{cases}$

となります。

以上より、

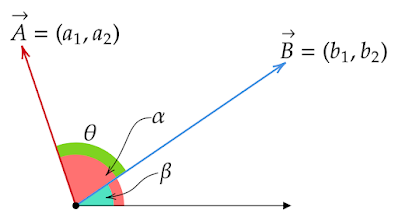
\vec{A}, \vec{B}

$\vec{\text{A}},\vec{\text{B}}$ それぞれの始点からx軸の正の方向にのびる直線と各ベクトルとのなす角を

α, β (α > β)

$α,β\ (α>β)$ とすると、

\begin{aligned} \cos α & = \frac{a_{1}}{\sqrt{{a_{1}}^{2} + {a_{2}}^{2}}}, \\ \sin α & = \frac{a_{2}}{\sqrt{{a_{1}}^{2} + {a_{2}}^{2}}} \\ \cos β & = \frac{b_{1}}{\sqrt{{b_{1}}^{2} + {b_{2}}^{2}}}, \\ \sin β & = \frac{b_{2}}{\sqrt{{b_{1}}^{2} + {b_{2}}^{2}}} \end{aligned}

$\begin{align*}\cos\alpha&=\frac{a_1}{\sqrt{{a_1}^2+{a_2}^2}},\\[0.5em]\sin\alpha&=\frac{a_2}{\sqrt{{a_1}^2+{a_2}^2}}\\[1em]\cos\beta&=\frac{b_1}{\sqrt{{b_1}^2+{b_2}^2}},\\[0.5em]\sin\beta&=\frac{b_2}{\sqrt{{b_1}^2+{b_2}^2}}\end{align*}$

となります。

θ = α - β

$θ=α-β$ であるから加法定理より

\begin{aligned} \cos θ & = \cos (α - β) \\ = \cos α \cos β + \sin α \sin β \\ = \frac{a_{1}}{\sqrt{{a_{1}}^{2} + {a_{2}}^{2}}} \cdot \frac{b_{1}}{\sqrt{{b_{1}}^{2} + {b_{2}}^{2}}} + \frac{a_{2}}{\sqrt{{a_{1}}^{2} + {a_{2}}^{2}}} \cdot \frac{b_{2}}{\sqrt{{b_{1}}^{2} + {b_{2}}^{2}}} \\ = \frac{a_{1} b_{1} + a_{2} b_{2}}{\sqrt{{a_{1}}^{2} + {a_{2}}^{2}} \sqrt{{b_{1}}^{2} + {b_{2}}^{2}}} \end{aligned}

$\begin{align*}\cosθ&=\cos(\alpha-\beta)\\[0.5em]&=\cos\alpha\cos\beta+\sin\alpha\sin\beta\\[0.5em]&=\frac{a_1}{\sqrt{{a_1}^2+{a_2}^2}}\cdot\frac{b_1}{\sqrt{{b_1}^2+{b_2}^2}}+\frac{a_2}{\sqrt{{a_1}^2+{a_2}^2}}\cdot\frac{b_2}{\sqrt{{b_1}^2+{b_2}^2}}\\[0.5em]&=\frac{a_1b_1+a_2b_2}{\sqrt{{a_1}^2+{a_2}^2}\sqrt{{b_1}^2+{b_2}^2}}\end{align*}$

よって

\begin{aligned} \vec{A} \cdot \vec{B} & = | \vec{A} | | \vec{B} | \cos θ \\ = \sqrt{{a_{1}}^{2} + {a_{2}}^{2}} \cdot \sqrt{{b_{1}}^{2} + {b_{2}}^{2}} \cdot \frac{a_{1} b_{1} + a_{2} b_{2}}{\sqrt{{a_{1}}^{2} + {a_{2}}^{2}} \sqrt{{b_{1}}^{2} + {b_{2}}^{2}}} \\ = a_{1} b_{1} + a_{2} b_{2} \end{aligned}

$\begin{align*}\vec{\text{A}}\cdot\vec{\text{B}}&=|\vec{\text{A}}||\vec{\text{B}}|\cosθ\\[0.5em] &=\sqrt{{a_1}^2+{a_2}^2}\cdot\sqrt{{b_1}^2+{b_2}^2}\cdot\frac{a_1b_1+a_2b_2}{\sqrt{{a_1}^2+{a_2}^2}\sqrt{{b_1}^2+{b_2}^2}}\\[0.5em]&=a_1b_1+a_2b_2\end{align*}$

となり、2式はどちらもベクトルの内積を表すことがわかります。

　別の方法として以下のようなものがあります。

　座標平面上のベクトル

\vec{X} = (x, y)

$\vec{\text{X}}=(x,y)$ をx成分のみのベクトル

\vec{X_{x}} = (x, 0)

$\vec{\text{X}_x}=(x,0)$ とy成分のみのベクトル

\vec{X_{y}} = (0, y)

$\vec{\text{X}_y}=(0,y)$ の2つに分解すると

\vec{X} = \vec{X_{x}} + \vec{X_{y}}

$\vec{\text{X}}=\vec{\text{X}_x}+\vec{\text{X}_y}$

となることから

\vec{a} = (a_{1}, a_{2}), \vec{b} = (b_{1}, b_{2})

$\vec{a}=(a_1,a_2),\vec{b}=(b_1,b_2)$ の内積は

\vec{a} \cdot \vec{b} = (\vec{a_{x}} + \vec{a_{y}}) \cdot (\vec{b_{x}} + \vec{b_{y}})

$\vec{a}\cdot\vec{b}=(\vec{a_x}+\vec{a_y})\cdot(\vec{b_x}+\vec{b_y})$

と書けます。

ここで、内積の分配法則

(\vec{A} + \vec{B}) \cdot \vec{C} = \vec{A} \cdot \vec{C} + \vec{B} \cdot \vec{C}

$(\vec{\text{A}}+\vec{\text{B}})\cdot\vec{\text{C}}=\vec{\text{A}}\cdot\vec{\text{C}}+\vec{\text{B}}\cdot\vec{\text{C}}$

を利用すると

\vec{a} \cdot \vec{b} = \vec{a_{x}} \cdot \vec{b_{x}} + \vec{a_{x}} \cdot \vec{b_{y}} + \vec{a_{y}} \cdot \vec{b_{x}} + \vec{a_{y}} \cdot \vec{b_{y}}

$\vec{a}\cdot\vec{b}=\vec{a_x}\cdot\vec{b_x}+\vec{a_x}\cdot\vec{b_y}+\vec{a_y}\cdot\vec{b_x}+\vec{a_y}\cdot\vec{b_y}$

と展開できます。

x軸とy軸は直交しているのでx成分のみのベクトルとy成分のみのベクトルのなす角は

90 °

$90°$ 、x成分のみのベクトル同士、y成分のみのベクトル同士のなす角は

0 °

$0°$ なので、

\begin{aligned} \vec{a} \cdot \vec{b} & = | \vec{a_{x}} | | \vec{b_{x}} | \cos 0 ° + | \vec{a_{x}} | | \vec{b_{y}} | \cos 90 ° + | \vec{a_{y}} | | \vec{b_{x}} | \cos 90 ° + | \vec{a_{y}} | | \vec{b_{y}} | \cos 0 ° \\ = a_{1} b_{1} + 0 + 0 + a_{2} b_{2} \\ = a_{1} b_{1} + a_{2} b_{2} \end{aligned}

$\begin{align*}\vec{a}\cdot\vec{b}&=|\vec{a_x}||\vec{b_x}|\cos0°+|\vec{a_x}||\vec{b_y}|\cos90°+|\vec{a_y}||\vec{b_x}|\cos90°+|\vec{a_y}||\vec{b_y}|\cos0°\\[0.5em]&=a_1b_1+0+0+a_2b_2\\[0.5em] &=a_1b_1+a_2b_2\end{align*}$

となり、ベクトルの内積の式を導くことができます。