ベクトルの平行条件 ~ 数学について考えてみる

2022年3月9日

ベクトルの平行条件

PLUMBAGO

　2つのベクトルが同じ向きであるか互いに反対向きであるとき、これらのベクトルは平行であるといいます。

⃗ A = (a_{1}, a_{2}), ⃗ B = (b_{1}, b_{2})

$\vec{\text{A}}=(a_1,a_2),\vec{\text{B}}=(b_1,b_2)$ の2つのベクトルが平行であるならば

\begin{matrix} ⃗ A & = k ⃗ B & (k : 実 数) a_{1} b_{2} - a_{2} b_{1} & = 0 \\ (a) (b) \end{matrix}

$\begin{align*}\vec{\text{A}}&=k\vec{\text{B}}&(k:実数)\tag{a}\\[0.5em]a_1b_2-a_2b_1&=0\tag{b}\end{align*}$

が成り立ちます。

ベクトルの実数倍はベクトルの向きは変わらないか逆向きになるので $\text{(a)}$ が平行なベクトル間で成り立つことはわかりますが、なぜ平行ならば $\text{(b)}$ が成り立つといえるのでしょうか？

　2通りの方法で確かめてみます。

1. 比例式

(a)

$\text{(a)}$ より

(a_{1}, a_{2}) = k (b_{1}, b_{2}) = (k b_{1}, k b_{2})

$(a_1,a_2)=k(b_1,b_2)=(kb_1,kb_2)$

なので、

\begin{matrix} a_{1} : b_{1} & = a_{2} : b_{2} a_{1} b_{2} & = a_{2} b_{1} a_{1} b_{2} - a_{2} b_{1} & = 0 \end{matrix}

$\begin{align*}a_1:b_1&=a_2:b_2\\[0.5em] a_1b_2&=a_2b_1\\[0.5em]a_1b_2-a_2b_1&=0\end{align*}$

となり、

(b)

$\text{(b)}$ が成り立つことがわかります。

2. $\sinθ$ の利用

　2つのベクトルが平行であるということは2つのベクトルのなす角が

0 °

$0°$ または

180 °

$180°$ であるということです。

この点に着目し

| ⃗ A | | ⃗ B | sin θ

$|\vec{\text{A}}||\vec{\text{B}}|\sinθ$

という式について考えます。

⃗ A, ⃗ B

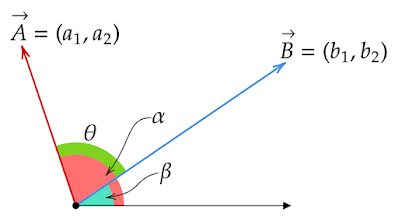
$\vec{\text{A}},\vec{\text{B}}$ それぞれの位置ベクトルを考え、x軸の正の方向にのびる半直線と各ベクトルとのなす角を

α, β

$α,β$ （ただし、

α > β

$α>β$ ）、

⃗ A

$\vec{\text{A}}$ と

⃗ B

$\vec{\text{B}}$ のなす角を

θ

$θ$ とすると、以下のようなことがわかります。

\begin{matrix} | ⃗ A | & = \sqrt{{a_{1}}^{2} + {a_{2}}^{2}}, | ⃗ B | & = \sqrt{{b_{1}}^{2} + {b_{2}}^{2}} cos α & = \frac{a_{1}}{\sqrt{{a_{1}}^{2} + {a_{2}}^{2}}}, sin α & = \frac{a_{2}}{\sqrt{{a_{1}}^{2} + {a_{2}}^{2}}} cos β & = \frac{b_{1}}{\sqrt{{b_{1}}^{2} + {b_{2}}^{2}}}, sin β & = \frac{b_{2}}{\sqrt{{b_{1}}^{2} + {b_{2}}^{2}}} \end{matrix}

$\begin{align*}|\vec{\text{A}}|&=\sqrt{{a_1}^2+{a_2}^2},\\[0.5em]|\vec{\text{B}}|&=\sqrt{{b_1}^2+{b_2}^2}\\[1em]\cos\alpha&=\frac{a_1}{\sqrt{{a_1}^2+{a_2}^2}},\\[0.5em]\sin\alpha&=\frac{a_2}{\sqrt{{a_1}^2+{a_2}^2}}\\[1em]\cos\beta&=\frac{b_1}{\sqrt{{b_1}^2+{b_2}^2}},\\[0.5em]\sin\beta&=\frac{b_2}{\sqrt{{b_1}^2+{b_2}^2}}\end{align*}$

$θ=\alpha-\beta$ となるので加法定理より

$\begin{align*}\sinθ&=\sin(\alpha-\beta)\\[0.5em]&=\sin\alpha\cos\beta-\cos\alpha\sin\beta\\[0.5em]&=\frac{a_2}{\sqrt{{a_1}^2+{a_2}^2}}\cdot\frac{b_1}{\sqrt{{b_1}^2+{b_2}^2}}-\frac{a_1}{\sqrt{{a_1}^2+{a_2}^2}}\cdot\frac{b_2}{\sqrt{{b_1}^2+{b_2}^2}}\\[0.5em]&=\frac{a_2b_1-a_1b_2}{\sqrt{{a_1}^2+{a_2}^2}\sqrt{{b_1}^2+{b_2}^2}}\end{align*}$

したがって、

$\begin{align*}|\vec{\text{A}}||\vec{\text{B}}|\sinθ&=\sqrt{{a_1}^2+{a_2}^2}\cdot\sqrt{{b_1}^2+{b_2}^2}\cdot\frac{a_2b_1-a_1b_2}{\sqrt{{a_1}^2+{a_2}^2}\sqrt{{b_1}^2+{b_2}^2}}\\[0.5em]&=a_2b_1-a_1b_2\end{align*}$

ここで、

$θ=0°,180°$ のとき

$\sinθ=0$ 、すなわち